图是很常见的一种构造了,不管是数据构造算法中的各种图构造,还是机器学习中的概率图。图紧张是由多少顶点及连接南北极点的边所构成的图形,通过它可以用来描述某些事物之间的某种特定关系。
有向无环图

有向无环图,即 Directed Acyclic Graph,属于有向图,图构造中不存在环,可用来表示事宜之间依赖关系。
Trie树
Trie 是一种搜索树,它的 key 都为字符串,通过 key 可以找到 value。能做到高效查询和插入,韶光繁芜度为O(k),缺陷是耗内存。它的核心思想便是减少没必要的字符比较,使查询高效率,即用空间换韶光,再利用共同前缀来提高查询效率。
Trie 树的根节点不包含字符,根节点到某节点的路径连起来的字符串为该节点对应的字符串,每个节点只包含一个字符,此外,任意节点的所有子节点的字符都不相同。
比如如下,将五个词语添加到 Trie 树中,末了的构造如图所示。
TrieTree tree = new TrieTree();
tree.put(\"大众美利坚\"大众);
tree.put(\公众俏丽\公众);
tree.put(\"大众金币\"大众);
tree.put(\"大众金子\公众);
tree.put(\"大众帝王\"大众);
双数组Trie
Trie 树的实现可以有多种方法,紧张的差异是存储构造的不同,不同的存储构造将导致占用空间不同。常见有定长数组办法、变长列表等。
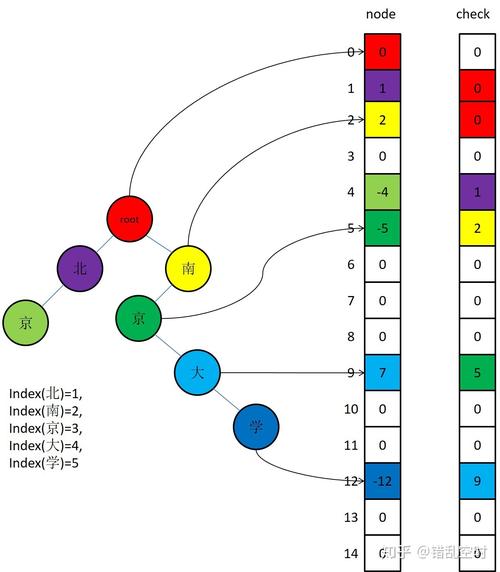
而个中有一种办法能让性能和占用空间都达到较好水平,这便是双数组办法,即双数组 Trie 树。双数组意思便是由两个数组来实现存储,分别为 base 和 check 数组,它们时两个相互平行的数组。
base 数组和 check 数组记录了所有转换状态,如果吸收了一个字符 c ,要从状态 s 移动到 t 的转移,则对应在双数组中的条件是:
check[base[s] + c] = s
base[s] + c = t
根据现有词典将所有状态都建立起来后,后面查询时则直接根据字与字之间的状态转换并根据 check 数组的值即可以判断是否已经完成单词的搜索,个中 base 数组紧张浸染是可以用来判断是否存在某些字到字的状态转换,而 check 数组则紧张用来判断是否是一个完全词语。
有向无环图浸染
比如对付这么个任务:存在一个大词典,要根据该词典找出一段文章包含的所有可能的词,这样就能从头到尾构建多少条路径,而且每个词对应的边都可能有不同的权重值,而终极将该段文章若何分词取决于哪个路径的值最小或者哪个路径走到终点的概率最大。
为了构建这个有向无环图,会涉及到遍积年夜量数据集的问题,这正是引入双数组 Trie 树的缘故原由,将耗时的搜索交给双数组 Trie 树,只须要从头到尾暴力匹配即能完成有向无环图的创建了。
连续优化?
引入 AC 自动机该当还能连续优化。
github
https://github.com/sea-boat/TextAnalyzer/blob/master/src/main/java/com/seaboat/text/analyzer/data/structure/DAGModel.java
















