徐龙威, 吴忠望, 董绪荣 航天工程大学航天信息学院, 北京 101416 择要:GLONASS伪距频间偏差难以利用履历模型肃清。在RTK定位解算中,尤其是需顾及大气延迟的中长距离异质基线,IFCB会降落模糊度收敛速率,乃至导致模糊度固定缺点。本文基于双差HMW组合和消电离层组合,提出一种站间IFCB实时估计算法,实时获取各频段的非组合站间单差IFCB。试验结果表明,站间IFCB长期稳定,可达数个纳秒;在GPS/GLONASS不雅观测值先验偏差比值为3:5的条件下,未改正的IFCB可能导致基线GPS/GLONASS组合RTK定位性能比单GPS差。将本文提出算法运用于RTK定位,能够有效肃清IFCB的影响,RTK模糊度浮点解精度、定位收敛速率和固定率都有明显改进,部分基线的RTK定位首次固定时间从9.2 s提高到2.1 s,固定解比率从84.5%提高到97.9%。 关键词:GLONASS 站间IFCB实时改正 GPS/GLONASS组合RTK XU Longwei, WU Zhongwang, DONG Xurong. A real-time estimating algorithm of GLONASS inter-frequency code bias and its application in RTK[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(2): 169-181. DOI: 10.11947/j.AGCS.2022.20200416 
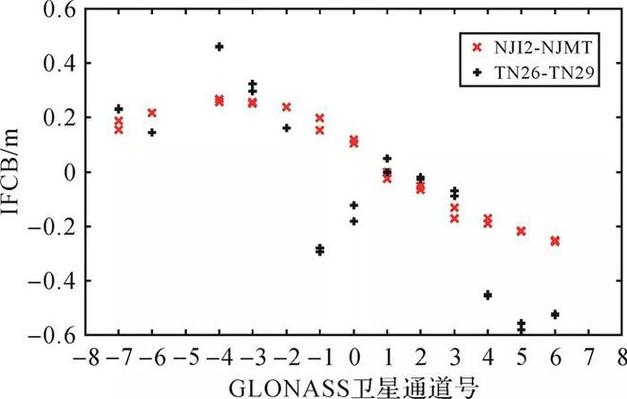
不雅观测值频间偏差(inter-frequency bias, IFB)一贯是影响GLONASS导航定位性能的主要成分。IFB紧张是源于同一频段(L1/L2)上不同GLONASS卫星的不雅观测旗子暗记硬件延迟差异[1]。在基于双差模型的基线解算中,不雅观测值站间单差能够肃清卫星端IFB,而吸收机端IFB受测站固件设备影响,难以直接肃清。按不雅观测值类型,IFB可划分为频间相位偏差(inter-frequency phase bias, IFPB)和频间码偏差(inter-frequency code bias, IFCB)[2]。文献[3-4]指出IFPB的实质是伪距不雅观测值和载波不雅观测值的硬件延迟之差,并将IFPB划分为数字旗子暗记处理引起的延迟和硬件本身引起的延迟两部分,且数字旗子暗记处理引起的延迟占紧张部分,因此,IFPB与旗子暗记频率和吸收机类型有很强的干系性。基于IFPB与旗子暗记频率的线性关系,许多学者采取估计IFPB变革率、构建纯载波不雅观测值组合等办法,实现了毫米级的IFPB改正,肃清IFPB对高精度定位的影响[5-9]。IFPB干系参数已经引入吸收机独立交流格式RINEX3.03文件和差分GNSS数据传输协议RTCM10403.X中,在导航定位做事中取得了良好的运用[10]。
IFCB紧张因吸收设备的前端带宽和干系器设计导致的芯片畸变产生,且每个旗子暗记通道的畸变量存在差异[11]。与能够高精度模型化的IFPB比较,IFCB的变革规律较为繁芜[12]。文献[13]采取精密单点定位模型估计了来自5家厂商的133台吸收机的非差消电离层组合IFCB,验证了吸收机或天线的品牌、系列和固件版本都会对IFCB的量级产生影响。文献[14-15]提出了组合不雅观测值的IFCB的估计策略,指出虽然IFCB与频率存在干系性,但难以构建通用的高精度线性模型,且个别测站的IFCB存在明显差异。综合多位学者的研究成果,IFCB的紧张特性可归纳为:①L1和L2上IFCB的量级不同,都具有一定的长期稳定性;②同质基线的IFCB量级相差很小,但也有一些特例存在;③异质基线的双差IFCB可达数米;④不同吸收设备的IFCB与通道号的线性关系不一致,导致IFCB无法采取统一模型改正。本文将GNSS旗子暗记吸收设备(吸收机类型、固件版本、天线类型)完备相同的测站构成的基线称为同质基线,其他基线统称为异质基线。
由于IFCB难以基于履历模型改正,在异质基线或精密单点定位解算中,常日将每颗卫星的IFCB或其与频率号干系的变革率作为一个静态参数估计。文献[13-15]将基于历史不雅观测值估计HMW或消电离层组合的IFCB用于GLONASS伪距组合不雅观测值实时改正。文献[16]直接将各颗卫星IFCB作为一个静态参数估计,进行载波不雅观测值变换合成超窄巷模糊度,实现长基线GLONASS模糊度固定,但该算法受限于不雅观测值噪声,仅能用于事后解算。文献[17]在RTK定位模型中,将IFCB与频率号干系的变革率作为静态参数进行估计,但从其结果来看,IFCB变革率参数估计策略显然是不符合IFCB特性的。文献[18]提出了一种用于精密单点定位消电离层组合的IFCB实时改正方法,能够明显改进GLONASS PPP定位的收敛速率和浮点解精度。德国地学研究中央(German Research Centre for Geosciences, GFZ)已经开始发布与吸收机类型干系的消电离层组合IFCB[19]。但是,上述研究都是针对不雅观测值组合的IFCB,且难以直接用于GLONASS实时非组合模糊度固定。尤其是异质基线的中长间隔RTK定位解算,伪距不雅观测值的IFCB可导致模糊度参数估计偏差,进而模糊度固定困难。
本文针对异质基线GLONASS双差IFCB难以肃清的问题,基于HMW组合和消电离层组合不雅观测值,提出一种非组合站间IFCB估计方法,对两个频段伪距不雅观测值的站间IFCB进行研究,并将该算法用于GPS/GLONASS组合RTK定位解算。须要指出的是,本文紧张对GLONASS IFCB特性进行研究,IFPB直接采取干系学者发布的先验值进行改正[5],见表 1。
表 1 各厂家的GLONASS IFPB变革率先验值Tab. 1 The priori corrections of GLONASS IFPB rate for receivers of different manufacturers
吸收机品牌IFPB变革率/cmTrimble-0.7Javad, JPS, TPS0.0Leica, Novatel2.3Septentrio4.9表选项
1.1 GLONASS站间IFCB估计方法
GLONASS双差不雅观测值可模型化为[5]
(1)
式中,P和L分别代表伪距和载波相位不雅观测值,单位为m;ρ表示卫星到测站的几何间隔;p和q为GLONASS卫星PRN,pq表示星间单差,q为参考星;m和n为基线测站编号,mn表示站间单差;T为对流层延迟;Imn, 1pq为第一频点上的双差电离层延迟;f1和f2为不雅观测值频率;τ为IFCB,ι为IFPB,单位为s;λ为载波波长;N为整周模糊度;ξ为多路径和不雅观测噪声;c为光速。GLONASS两个单差模糊度转化为一个双差和一个单差模糊度。由于GLONASS频分多址旗子暗记不同卫星的同一频段载波波长相差很小,在毫米级,即λip-λiq量级很小,单差模糊度可以直接取近似值引入不雅观丈量。
双差HMW(Hatch-Melbourne-Wübbena)组合可分解为一个双差伪距窄巷组合(narrow-lane, NL)和一个双差宽巷载波组合(wide-lane, WL),顾及GLONASS IFB的影响,HMW组合可模型化为[15, 20]
(2)
(3)
(4)
式中
(5)
(6)
(7)
综合式(2)-式(7)可获双差IFCB的窄巷组合,如式(8)所示
(8)
式中,单差宽巷模糊度可以通过伪距不雅观测值和载波不雅观测值做差直接得到。文献[21]中给出了GLONASS宽巷模糊度实时固定方法,IFPB采取先验值改动,于是式(8)等号右侧部分可以实时获取。
GLONASS双差伪距不雅观测值消电离层组合可表示为
(9)
式中,IF表示消电离层组合;等号右侧部分,GNSS RTK定位精度一样平常能够快速收敛到分米乃至厘米级,得到分米级以上精度的双差星地几何间隔ρmnpq;采取GTP2w模型估计,可以得到厘米级精度的对流层干延迟[22-23];IFPB可基于先验信息改正。因此,式(9)右侧部分也能够实时获取。
将对流层湿延迟模型化为天顶对流层湿延迟和VMF1映射函数,可得式(10)
(10)
式中,Tmnpq为对流层模型打算量;
基于式(8)和式(10),可得一个GLONASS卫星非组合双差IFCB解算方程
(11)
通过矩阵转换,可将双差IFCB参数变换为站间单差IFCB,如式(12)所示
(12)
为肃清方程秩亏,将参考卫星各频段(P1、P2)站间IFCB为0,测站间天顶方向对流层湿延迟即是0,3个条件作为虚拟不雅观测值引入模型,可得非组合站间IFCB的估计模型
(13)
1.2 站间IFCB实时改正的RTK定位解算流程
常规GNSS的RTK函数模型[9]为
(14)
式中,δPmn.ipq和δLmn.ipq表示双差伪距和载波非组合不雅观测值残差;lp为卫星到流动站的方向余弦向量;mp为对流层延迟映射函数;dx、
综合式(1)和式(14)可知,若RTK函数模型未顾及GLONASS站间IFCB,站间IFCB与电离层参数具有干系性,式(14)中电离层和模糊度参数的含义为
(15)
(16)
对付忽略大气延迟参数的短基线RTK,站间IFCB也会影响流动站坐标改正参数的估值,导致模糊度参数收敛速率减缓。
基于上文的GLONASS站间IFCB估计方法,本文提出一种实时改动GLONASS站间IFCB的RTK定位解算模型,如式(17)所示。利用文献[21]的中长间隔基线解算模型,进行GPS/GLONASS组合RTK定位,得到GLONASS宽巷整周模糊度和流动站近似坐标,实时估计GLONASS站间IFCB。并将宽巷模糊度作为RTK定位解算的未知参数,构建RTK定位模型,实现站间IFCB改正和RTK定位同步进行
(17)
式中,k为历元编号;[ΔL1k ΔL2k ΔP1k ΔP2k]T为当前历元的双频不雅观测值残差向量;C为卫星到流动站的方向余弦向量;a1k和a2k为对角矩阵diag(λ11λ12 … λ1α)和diag(λ21λ22 … λ2α),α为可见卫星数;I为α×α单位矩阵,Mp为卫星的天顶对流层湿延迟映射函数向量;dx、
图 1给出了站间IFCB实时改正的RTK定位解算流程,可划分为以下4个步骤:
图 1 站间IFCB实时改正的RTK定位解算Fig. 1 Real time inter-station IFCB correction algorithm in RTK图选项
(1) 采取式(17)进行RTK定位解算,如果已经改正IFCB,直接输出定位结果,结束当前历元解算。
(2) 若未改正IFCB,则输出双差星站间距和宽巷模糊度固定解,分别与GLONASS伪距双差消电离层组合和HMW组合一起,基于式(8)和式(10),得到双差IFCB窄巷组合和消电离层组合不雅观丈量。
(3) 基于双差站间IFCB宽巷组合和消电离层组合,引入参考星“零基准”和站间天顶对流层延迟虚拟不雅观测值,构建式(13)模型,滤波估计站间IFCB,实时改正GLONASS双差伪距不雅观测值。
(4) 站间IFCB改正后,重新开始步骤(1)的解算,输出RTK定位结果。
本文在基线长度小于20 km的RTK定位中忽略大气延迟的影响,中长间隔的RTK定位将大气延迟作为参数进行估计。对流层延迟先利用履历模型改正干分量、湿分量作为未知参数估计。将各颗卫星L1的双差电离层延迟作为未知参数估计且历元间不干系。
2.1 试验解释
试验数据源为欧洲区域参考框架连续GNSS不雅观测网络(EUREF permanent GNSS network, EPN)24个基准站的不雅观测数据(http://www.epncb.oma.be/index.php)[24],构建12条基线进行RTK定位解算,见表 2。12条基线中BS10为同质基线,其他基线为异质基线。基线长度分布在0~130 km,BS01-BS03基线长度小于5 km;BS04-BS12基线长度在20 km以上。
表 2 基线的测站吸收机和天线信息Tab. 2 Receiver and antenna on the two ends of baselines
基线名基准站吸收机天线流动站吸收机天线基线长/kmBS1GOPETRIMBLE ALLOY 5.44TPSCR.G3 TPSHGOP6SEPT POLARX5 5.3.2SEPCHOKE_B3E6 SPKE0.004BS2MAR6SEPT POLARX5 5.3.0AOAD/M_T OSODMAR7TRIMBLE ALLOY 5.43LEIAR25.R3 LEIT0.011BS3MET3JAVAD TRE_3 DELTA 3.7.7JAVRINGANT_DM SCISMETGTRIMBLE NETR9 5.43TRM59800.00 SCIS2.8BS4PASALEICA GR30 4.31/7.403LEIAR20 LEIMSCOALEICA GR25 4.31TRM55971.00 NONE22.1BS5PADOSEPT POLARX5 5.3.2SEPCHOKE_B3E6 SPKEVEN1LEICA GR30 4.20LEIAR20 NONE35.0BS6BCLNLEICA GR10 3.11.1639/6.524LEIAR25.R4 LEITBELLLEICA GR50 4.31/7.403LEIAR25.R4 NONE55.0BS7DENTSEPT POLARX4 2.9.6TRM59800.00 NONEVLISLEICA GR50 4.31/7.403LEIAR25.R4 LEIT58.4BS8HEL2LEICA GR50 4.31.101/7.403LEIAR25.R4 LEITRANTJAVAD TRE_3 DELTA 3.7.9LEIAR25.R4 LEIT74.5BS9TERSSEPT POLARX4 2.9.6LEIAR25.R4 LEITBORJJAVAD TRE_3 DELTA 3.7.9LEIAR25.R4 LEIT99.1BS10CRAKLEICA GR30 4.31/7.403LEIAR25.R4 EITCTABLEICA GR30 4.31/7.403LEIAR25.R4 LEIT103.3BS11TOILLEICA GR25 4.31/6.713LEIAR25.R4 LEITVIR2JAVAD TRE_3 DELTA 3.7.7JAVRINGANT_DM SCIS126.0BS12LEONLEICA GR25 3.11.1639LEIAR25 NONEVALALEICA GR30 4.31/7.403LEIAR25.R3 NONE127.6表选项
本文进行了站间IFCB估计及特性剖析、实时改正站间IFCB的RTK定位两个试验,其详细试验设置如下:
(1) 站间IFCB估计及特性剖析试验。基于2020年DOY 100-DOY 119,20 d,采样间隔30 s,GPS/GLONASS不雅观测数据估计站间IFCB并对其特性进行剖析。采取参数可变的序贯最小二乘平差算法估计站间IFCB和测站间天顶对流层湿延迟参数。站间IFCB作为不随韶光变革的恒定参数,天顶对流层湿延迟的过程噪声采取随机游走模型表示。顾及GLONASS伪距IFCB的影响,试验设定GLOANSS伪距的先验噪声为0.5 m,GPS伪距先验噪声为0.3 m,GPS和GLONASS载波相位的先验噪声为0.003 m;不雅观测值高度角定权策略为P=1, el>30°; P=sin(el), el≤30°[14, 25]。卫星高度角阈值为7°。由于各颗卫星的站间IFCB估值是基于一定基准的相对值,如果以双差解算的参考星为基准,解算过程中参考星的变换会导致站间IFCB的数值变革。为便于统计剖析,站间IFCB单天解估计选取所有可见卫星各频段的站间IFCB之和即是0为基准,以确保全体解算过程的基准统一。
(2) 实时改正站间IFCB的RTK定位试验。利用2020年DOY 119的24 h,采样间隔1 s,GPS/GLONASS不雅观测数据验证本文GLONASS站间IFCB实时改正算法对RTK定位解算的影响。不雅观测值噪声、高度角定权和阈值、对流层延迟估计、站间IFCB估计等策略与试验(1)相同。以参考星的站间IFCB为0作为基准。RTK模糊度解算采取分步固定的部分模糊度固定策略。首先,采取取整算法固定宽巷模糊度,取整阈值为0.25周,浮点解理论成功率大于99.9%。其次,基于宽巷模糊度固定解更新解算方程,采取LAMBDA算法搜索窄巷模糊度,并进行ratio考验[26],ratio阈值设为2.5。如果模糊度搜索未通过ratio考验,则删除搜索区域中高度角最低卫星的模糊度,重新搜索,直到通过ratio考验。RTK定位过程中,当前历元仅继续上一历元的浮点解,滤波解算后,重新进行模糊度搜索固定,以避免继续上一个历元缺点的固定解。
为验证实时站间IFCB算法可行性,本文采取单GPS、未改正站间IFCB的GPS/GLONASS组合,以及实时改正站间IFCB的GPS/GLONASS组合3种RTK定位模式,分别以G、GRuc-IFCB和GR rtc-IFCB表示。RTK定位解算每小时初始化一次,统计其收敛韶光、首次固定时间、模糊度固定率和定位偏差等指标。
2.2 站间IFCB估计结果和特性剖析
图 2给出了GLONASSR01卫星两个频段伪距(P1和P2)的站间IFCB单天解韶光序列。各条基线站间IFCB存在明显差异,一些基线的站间IFCB靠近3 ns,如基线BS06、BS09、BS12的P2站间IFCB。同一条基线P1和P2站间IFCB的量级存在很大差异,如基线BS04 P1站间IFCB约-0.4 ns,而P2站间IFCB达到2.6 ns。同质基线BS10的站间IFCB估值明显比异质基线小,其P1和P2上站间IFCB估值均小于0.3 ns。站间IFCB单天解估值具有一定的稳定性,如图 3所示,所有基线的GLONASSR01卫星单天解的标准差均小于0.3 ns。受多路径等未模型化偏差的影响,基线BS02 P1和基线BS05 P2的站间IFCB标准差较大,分别约0.24 ns和0.28 ns。
图 2 GLONASS R01卫星站间IFCB单天解估值的韶光序列Fig. 2 Daily estimate values of GLONASS R01 inter-station IFCB图选项
图 3 GLONASS R01卫星站间IFCB单天解估值的标准差Fig. 3 Standard deviation of daily GLONASS R01 inter-station IFCB
图选项
图 4中给出了所有基线各颗GLONASS卫星的站间IFCB单天解估值均值。图 4中信息能够证明基于图 2和图 3获取的结论具有普适性。以卫星R14为例,基线BS09 P1站间IFCB的量级靠近6 ns;基线BS09和BS05的P1站间IFCB之差约10 ns。基线BS01 R12卫星P1站间IFCB小于-0.3 ns,而其P2站间IFCB靠近-4 ns。同质基线所有卫星的站间IFCB估值分布在[-0.6, 0.6] ns区间内。
图 4 各颗GLONASS卫星站间IFCB单天解均匀值Fig. 4 The averages of GLONASS inter-station IFCB daily estimate values图选项
图 5给出了R09卫星改正站间IFCB前后的伪距不雅观测值残差。由图 5可知,BS01 P1、BS05 P1、BS09 P1、BS09 P2都存在明显的系统性偏差。例如,BS09 P2的残差分布在区间[0, 5] m之间,均值在2.3 m旁边。由于参考卫星的变换,BS05 P1残差在两个不雅观测时段的系统偏差项不同。改正站间IFCB往后,所有卫星的伪距残差分布区间明显向0平移,BS05伪距残差在两个不雅观测时段的分布区间差异也被肃清。
图 5 卫星R09改正站间IFCB前后的伪距不雅观测值残差Fig. 5 Residual errors of R09 pseudorange observations before and after IFCB correction图选项
2.3 站间IFCB改正对RTK定位的影响
站间IFCB导致异质基线双差伪距不雅观测值的系统性偏差,影响RTK定位结果。由于IFCB与吸收机类型、固件版本和天线类型干系的繁芜特性,乃至同质基线也可能存在系统性偏差。因此,须要采取与吸收设备无关的实时校正算法,实现伪距不雅观测值系统性偏差的肃清。
图 6给出了短基线BS01、中间隔基线BS05和长间隔基线BS09的R01、R07和R08 3颗GLONASS卫星站间IFCB实时估值的韶光序列。试验数据不雅观测时段2020年DOY 119 UTC 06∶00-06∶30,采样间隔为1 s,每5 min进行一次站间IFCB重新初始化解算。由图 6可知,站间IFCB估值通过约30 s序贯最小二乘平差迭代即可得到分米级的精度,1 min内完成收敛。因此,将迭代1 min的站间IFCB估值用于改动GLONASS伪距不雅观测值具有可行性。
图 6 基线BS09GLONASS卫星站间IFCB实时估值韶光序列Fig. 6 Time series of GLONASS inter-station IFCB estimates on baseline BS09图选项
采取G、GR uc-IFCB和GR rtc-IFCB 3种模式分别进行RTK定位解算。图 7和图 8给出了基线BS01和BS09的GLONSS和GPS卫星模糊度浮点解偏差。短基线RTK场景下,忽略了双差大气延迟的影响,GLONASS站间IFCB在解算过程中紧张归入残差向量,须要通过更永劫光的滤波,才可以得到准确的模糊度浮点解。因此,短基线BS01,未改正站间IFCB时,GLONASS卫星须要约6 min韶光才能得到稳定的高精度模糊度参数浮点解,站间IFCB实时改正算法可将收敛韶光缩短到3 min以内;如图 8左侧图所示,改正站间IFCB可以明显加快GPS卫星模糊度浮点解收敛。在中长基线RTK场景下,需估计电离层和对流层延迟参数,由于电离层参数与站间IFCB的强干系性,导致电离层参数估值产生偏差,进而影响模糊度浮点解。改动GLONASS伪距不雅观测值对中长基线RTK定位至关主要,可有效肃清估计参数偏差,改进模糊度准确度,提高模糊度固定率和RTK定位性能。
图 7 GLONSS卫星宽巷和窄巷模糊度浮点解偏差Fig. 7 The bias of GLONASS satellite wide-lane and narrow-lane ambiguity float solutions图选项
图 8 GPS卫星G13宽巷和窄巷模糊度浮点解偏差Fig. 8 The bias of GPS satellite G13 wide-lane and narrow-lane ambiguity float solutions
图选项
图 9统计了所有基线不同模型RTK解算模式下的收敛韶光。本文将RTK定位水平方向偏差稳定在小于0.1 m作为剖断收敛完成的阈值[14, 27]。基线BS04、BS08和BS09受站间IFCB的影响,GPS/GLONASS组合RTK定位收敛速率较单GPS RTK定位变慢。站间IFCB实时改正后,GPS/GLONASS组合RTK收敛速率明显加快,大部分基线的收敛韶光减小到单GPS RTK的60%以下,办理了因引入GLONASS卫星导致异质基线收敛速率降落的问题。站间IFCB改正算法对同质基线BS10 GPS/GLONASS组合RTK定位收敛韶光的影响很小。基线BS06因流动站数据质量较差,定位收敛速率较慢,单GPS RTK须要约90 s完成收敛。
图 9 不同模式RTK解算的收敛韶光Fig. 9 Convergence time of RTK positioning solutions图选项
采取式(18)和式(19)统计模糊度固定成功率Psuc和精确率Pcor
(18)
(19)
式中,namb为解算中模糊度参数的总数;nfixed为固定的模糊度参数个数;ncorrect为精确固定的模糊度参数个数。
站间IFCB改正能够显著提高中长间隔基线的GPS和GLONASS卫星模糊度固定成功率和精确率,如图 10和图 11所示。站间IFCB导致基线BS09的GLONASS卫星窄巷模糊度固定成功率低至52%,改正落后步到约90%,模糊度固定精确率也从85%提高到96%。短基线(BS01-BS04),双差大气延迟量级较小,可忽略,模糊度固定随意马虎,改正站间IFCB对模糊度固定的影响不大。但是,当站间IFCB量级很大时,改正站间IFCB对提高模糊度固定效率十分必要。
图 10 RTK定位解算模糊度参数固定成功率Fig. 10 The successful fixing rates of ambiguity parameters in RTK solution图选项
图 11 RTK定位解算模糊度参数固定精确率Fig. 11 The correct fixing rates of ambiguity parameters in RTK solution
图选项
采取分步部分模糊度固定策略得到RTK固定解,统计其首次固定时间、固定解比率和固定解偏差RMS,如图 12和图 13所示。以EPN网站发布的坐标值作为参考站和流动站坐标的真值。与上文试验结果类似,站间IFCB改正算法能够明显改进中长间隔基线GPS/GLONASS组合RTK定位性能。比较单GPS,站间IFCB导致基线BS09的GPS/GLONASS组合RTK首次固定时间变长且固定解比率降落。进行站间IFCB改正后,首次固定时间统计值从9.2 s提高到2.1 s,固定解比率从84.5%提高到97.9%。由于短基线RTK能够实时得到固定解,站间IFCB改正对定位结果的影响不明显。改正站间IFCB后,模糊度固定率提高,RTK固定解的定位偏差也有不同程度的改进。如基线BS12东北天方向的定位偏差RMS分别从2.5、2.8、6.1 cm提高到2.3、2.4、5.0 cm,个中高程方向改进率达18%。
图 12 RTK定位首次获取固定解韶光和固定解比率Fig. 12 Time to first fixed and rates of RTK fixed solutions图选项
图 13 RTK定位固定解ENU方向的RMSFig. 13 Positioning bias RMS of RTK fixed solutions on E/N/U direction
图选项
本文提出了一种不依赖测站设备信息的站间IFCB实时估计方法,对GLONASS卫星各频段站间IFCB进行了特性剖析,并将站间IFCB实时改正算法运用于GPS/GLONASS组合RTK定位,得到了以下结论:
(1) 站间IFCB单天解具有一定的稳定性,20 d内单天解估值的标准差小于0.3 ns,同一条基线不同频段站间IFCB的量级存在很大差异,可达几个纳秒。站间IFCB会导致异质基线RTK解算模糊度固定失落败,乃至个别基线GPS/GLONASS组合定位的性能比单GPS差。
(2) 将站间IFCB实时估计算法用于GPS/GLONASS组合RTK定位,能够显著改进GPS/GLONASS组合RTK定位性能。对付受站间IFCB影响严重的基线,算法能够将GLONASS卫星窄巷模糊度固定成功率从52%提高到90%以上,东北天方向的定位偏差RMS分别从2.5、2.8、6.1 cm提高到2.3、2.4、5.0 cm。
第一作者简介:徐龙威(1988-), 男, 博士, 讲师, 研究方向为多模GNSS高精度定位。E-mail: xlw_ltu2012@163.com
往期推举
资讯
○《测绘通报》企业招聘季直播,精彩即将开启!
○ 武汉大学发布2022年硕士研究生招生考试复试基本分数线!
○ 国际华人地理信息科学协会 CPGIS Awards 2022 名誉奖开始提名
○ 5大省地震局2022年度公开招聘
○ 快来!
自然资源部这些单位招聘啦
○ 司南导航2022春招全面启动
会议
《测绘学报》
○ 测绘学报 | 赵庆志:GNSS约束的MERSI/FY-3A PWV校准方法
○ 测绘学报 | 张玉鑫:高分辨率遥感影像建筑物提取多路径RSU网络法
○ 测绘学报 | 余俊鹏:附加傅里叶补偿项的卫星遥感影像RFM平差方法
○ 测绘学报 | 许彪:分区优化稠浊SfM方法
《测绘通报》
○ 《测绘通报》2022年第1期目录
○ 《测绘通报》2022年第2期目录
○ 地市级实景三维城市培植及运用
○ 像控点布设对勘测定界繁芜区域实景建模精度的影响
《北京测绘》
○《北京测绘》2022年第1期择要推举
○《北京测绘》2021年第12期择要推举
○《北京测绘》2021年第11期择要推举
○《北京测绘》2021年第10期择要推举
《测绘科学技能学报》
○ 择要 |《测绘科学技能学报》2021年第2期择要推举
○ 择要 |《测绘科学技能学报》2021年第4期择要推举
○ 择要 |《测绘科学技能学报》2021年第5期择要推举
○ 择要 |《测绘科学技能学报》2021年第6期择要推举
《地球信息科学学报》
○ 《地球信息科学学报》2022年第3期佳文推介
○ 龚健雅院士:环球位置信息叠加协议与位置做事网技能研究进展与展望
○ 佳文推介 | 大数据城市通勤交通模型的构建与仿照运用
○ 专刊征稿:社会感知与地理大数据挖掘(征稿中)
《测绘工程》
○ 择要 |《测绘工程》2021年第5期择要推举
○ 择要 |《测绘工程》2021年第6期择要推举
○ 择要 |《测绘工程》2022年第1期择要推举
○ 佳文推介 | 单目视觉技能在室内定位中的运用研究
《中国空间科学技能》
○ 火卫二地形地貌探测综述
○《中国空间科学技能》2022年第1期择要
○《中国空间科学技能》2021年第6期择要
○《中国空间科学技能》2021年第5期择要推举
《卫星运用》
《Journal of Geodesy and Geoinformation Science》
○《测绘学报(英文版)》专刊征稿 | 舆图学与地球空间信息教诲:理论与实践
○ 《测绘学报(英文版)》专刊征稿 | 用于三维地理信息的拍照丈量和打算机视觉
○ Xiang LI et al. | 《测绘学报(英文版)》(JGGS)精选论文
○ Xinchang ZHANG et al. | 《测绘学报(英文版)》(JGGS)精选论文
《Satellite Navigation》
○ 徐元博士:面向有色丈量噪声下UWB/INS组合行人导航的分布式卡尔曼滤波| SANA佳文速递
○ 杨飞博士:GNSS天顶对流层精化模型的构建与剖析| SANA佳文速递
○ 姚铮教授:北斗PPP做事旗子暗记调制复用方案设计与质量评估| SANA佳文速递
○ 2022征文| SatNav“普适定位、室内导航与基于位置做事”专题
《自然资源遥感》
○ 《自然资源遥感》入驻“智绘科服”融媒体平台!
○ 《自然资源遥感》征稿:“海岸带空间资源及生态康健遥感监测”专栏
○ 择要 |《自然资源遥感》2021年第3期择要推举
○ 择要 |《自然资源遥感》2021年第4期择要推举
《Journal of Geovisualization and Spatial Analysis》
○《Journal of Geovisualization and Spatial Analysis》入驻“智绘科服”融媒体平台!
○ JGSA国际期刊2021年第5卷第2期论文择要
○ 高被引论文推举 | Journal of Geovisualization and Spatial Analysis
《环球定位系统》 ○ 《环球定位系统》论文推举 | 刘光明:我国常用地心坐标系的现状与发展
















