其余像我们家里的族谱,或者说是我们的家庭构造,也是一个范例的树构造。此外,在打算机领域,我们每天要打交道的【文件夹】、数据库中我们存储的数据,都是树的范例的运用。本日我们来学习的便是比较偏理论的关于树和二叉树的定义以及它们的一些属性特点。
树从上面实际生活中的例子里,我们可以看出,树这种构造是可以归纳出它的一些特点的。

树 (Tree)是 N (N>0)个结点的有限集,它或为空树(N=0);或为非空树 T 。
在这个定义中,我们须要明确两个问题:一是树一定是有结点的,二是根据结点数量可以分为空树和非空树两种。不过这只是最基本的定义,它还有一些特性。
有且仅有一个称之为根的结点。
也便是说,这个树一定是从某一个结点开始扩展出来的,这个结点就向树根一样。从它开始向外开枝散叶。
除根结点以外的别的结点可分为 m ( m > 0 ) 个互不相交的有限集 T1,T2 ……,Tm 个中每一个凑集本身又是一颗树,并且称为根的子树(SubTree)
这一段可能会不太好理解,实在说白了便是每个结点只有一个上级结点,不能有多个上级结点。同理,平级结点之间也不能有联系,但是它可以有多个下级结点。
关于树的定义我们可以看下下面这个图。
上图中大略的列举了标准的树和不标准的树是什么样子的。个中:
(a) ,是只有一个根结点的树,只要有一个结点,它就可以称为一个树构造
(b) ,是一个标准的树构造
(c) ,把稳它的 C 和 H 结点之间有一条连接线,这个就不是树了,结点只能有一个上级结点的才称为树,这个实在便是我们将来要学的【图】了
树的干系术语相对付栈的压(入)栈、出栈,行列步队的入队、出队来说,树的干系术语可就繁芜的多了。不论如何,首先你得先记住这些术语,要不后面讲的东西用得那些术语只会让你更晕。不过我们一时记不住也没紧要,先有个大概的印象,在后面的学习进程中碰着了再回来复习,这样印象反而会更加深刻。
结点:一个结点可能包含一组数据,或者指向其它结点的分支,可以看作是树枝分叉的那个地方,(b)图中 A、 B、 C、 D、 E 等等这些都是结点
结点的度:结点拥有的子树数量就叫做结点的度,实在便是它的下级子结点有几个便是几度,(b)图中,C 结点的度为 1 , D 结点的度为 3
树的度:树内各结点度的最大值,便是拥有最多子结点的度是多少,这个树的度便是多少,(b) 图这个树的度为 3
叶子:度为0的结点,也便是没有子结点的结点,(b) 图中的 K 、 L 、 F 、 G 、 M 、 I 、 J 便是这颗树的叶子结点
双亲和孩子:一个结点的子结点,便是它的孩子;对付这些子结点来说,当前这个结点便是它的双亲,(b) 图中,D 的孩子是 H 、 I 、 J ,而 H 、 I 、 J 的双亲便是 D
层次:从根结点算起,根结点便是第一层,根的孩子便是第二层,依次类推,(b) 图中 G 结点所在的层次为 3 ,(a) 图的全部层次都只有 1
树的深度(高度):当前这颗树的最大层次,很明显,(b) 图的深度便是 4
兄弟、先人和子孙:兄弟结点便是这些结点的双亲是同一个结点;先人结点便是从根结点到某个指定结点路上的经由的所有结点;子孙便是从某一个节点出发,到达目标结点这一起上的所有结点。(b) 图中, E、 F 是兄弟,E 的先人是 A 、 B , E 的子孙为 K 或者 L
堂(表)兄弟:所有在同一层的结点但双亲不同的结点都是堂兄弟,同样还是在 (b) 图中,G 的堂(表)兄弟有 E、 F ,其余还有 H 、 I 、 J 也是它的表兄弟
二叉树对付树的观点有了一定的理解之后,我们再来进一步的学习另一个观点,同时也是在数据构造和算法中最主要的一种树的形式:二叉树。
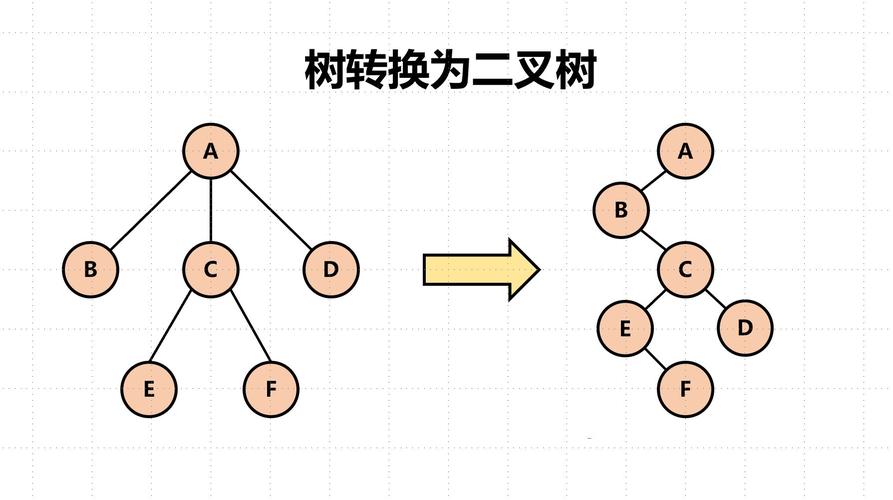
常日来说,树的形态是可以千变万化的,比如一个结点可以有 3 个子结点,而另一个结点可能有 300 个子结点。这样没有什么规则的树实在操作起来会非常麻烦,而二叉树的定义就要大略的多,除了有树的性子外,它还多了一项内容:二叉树的每个结点最多只有两个子结点,也便是说,全体二叉树的度肯定是 2 ,所有结点的度也不会超过 2 。关于二叉树为什么好操作这点,我们不才一小节的二叉树的性子中再详细地解释。所有的树构造都是可以通过一定的规则变形来转换成二叉树的。
我们同样还是通过一张图示来展示什么是二叉树。
二叉树中,左边的子结点及其子孙结点可以算作是关于当前结点的左子树。右边结点及其子孙结点也一样可以算作是当前结点的右子树。根据结点的子结点情形,就有了上面图中的这几种二叉树形态。
(a) 树是仅有一个结点的树,也可以说是仅有一个结点的二叉树
(b) 树是仅有一个左结点的二叉树
(c) 树是仅有一个右结点的二叉树
(d) 树是拥有旁边两个结点的二叉树
二叉树的性子性子1:在二叉树的第 i 层上至多有 2i-1 个结点( i >= 1 )
性子2:深度为 k 的二叉树至多有 2k - 1 个结点( k >= 1)
性子3:对任何一颗二叉树 T ,如果其终端结点数为 n0 ,度为2的结点数为 n2 ,则 n0 = n2 + 1
性子4:具有 n 个结点 的完备二叉树的深度为 log2n + 1
性子5:如果对一颗有 n 个结点 的完备二叉树(其深度为 log2n + 1 )的结点按层序编号(从第1层到第 log2n + 1 层,每层从左到右),则对任一结点 i ( 1 <= i <= n),有:
如果 i = 1 ,则结点 i 是二叉树的根,无双亲;如果 i > 1 ,则其双亲是结点 i / 2
如果 2i > n ,则结点 i 无左孩子(结点 i 为叶子结点);否则其左孩子是结点 2i
如果 2i + 1 > n ,则结点 i 无右孩子;否则其右孩子是结点 2i + 1
关于二叉树的上述五个性子的数学证明我们就不详细说了,毕竟我们这一系列的文章的宗旨也是希望通过大略的示例让大家学习到数据构造和算法的精髓,而不是大略粗暴的直接用数学公式来推导证明,那么我们就直接来图上数一数就好了。
对付 性子1 来说,我们当前这个二叉树根据公式的话,在第 3 层上最多只能有 23-1 个结点,也便是 4 个结点。第 4 层上最多只能有 24-1 ,也便是 23 = 8 个结点
对付 性子2 来说,当前这图中的树的深度为 4 ,也便是最多有 24 - 1 = 15 个结点
性子3 的话,我们先数数度为 2 的结点有多少,在这个图中,度为 2 的结点有 7 个,也便是 A 、 B 、 C 、 D 、 E 、 F 、 G ,第 4 层的结点都是没有子结点的,也便是说它们都是 0 度的,也称为终端结点(叶子结点),这些结点的数量一共是 8 个。现在 n2 = 7 ,根据性子公式就可以得出 n0 = n2 + 1 = 7 + 1 = 8
图中的结点数量为 15 个,套用 性子4 的公式可以得出 log2n + 1 = log215 + 1 = 3.91(向下取整) + 1 = 3 + 1 = 4 ,当前树的深度即为 4 ,性子4 和 性子2 可以看作是互补的
对付 性子5 来说,请把稳每个结点边上的编号,我们就选取 E 结点来作为例子解释。E 结点当前为 5 ,以是它的双亲为 5 / 2 = 2 (向下取整);E 的左孩子为 2i ,也便是 25=10 ,E 的右孩子为 2i + 1 ,也便是 25+1 = 11;性子5 的定义中说得更抽象一些,而且是拿叶子结点来做解释的,针对的是全体二叉树的情形,但实在意思和我们这里阐明的是一样的,大家可以再拿其它结点验证一下。性子5 对付后面我们要讲的利用顺序构造来存储二叉树非常主要!
请务必节制并记牢二叉树的这五个性子及其含义,由于在后面的学习中,不管是二叉树的顺序、链式存储构造,还是二叉树的遍历,都有可能会打仗到上面的五个性子中的内容。可以说,它们便是二叉树学习中最最根本的灵魂。
森林末了,我们来大略的理解下什么是“森林”。多个树放在一起,就形成了一片“森林”。就像上文中二叉树的阐明图一样,(a)(b)(c)(d)放在一起将它们整体一起来看,便是一片“森林”,在这片“森林”等分别有着(a)(b)(c)(d)这四颗树。森林中的树和树之间是没有联系的,如果我们要操作或者遍历一个森林的话,每每是将这片森林转化为一颗树。详细的算法和步骤不是我们学习的重点,以是大家理解一下即可,有想深入研究的同学可以搜索干系的内容或者查阅干系的教材。
总结从栈和行列步队提高到树后,是不是溘然觉得到一下子就迈了一大步?有点搞不懂了?没紧要,本日的内容实在都是一些根本的理论内容,能理解的就理解,不能理解的就接着连续学习之后再返过来看本日的这些观点。学习就不不断地重复进步地过程,当然统统都还是要以地基为根本的。当你理解了树的数据构造及一些大略的遍历算法之后,再回来深入的理解这些观点并把他们背下来,相信一样平常的口试中关于树干系的题目就不在话下了,一起努力吧!
参考资料:
《数据构造》第二版,严蔚敏
《数据构造》第二版,陈越
《数据构造高分条记》2020版,天勤考研
















