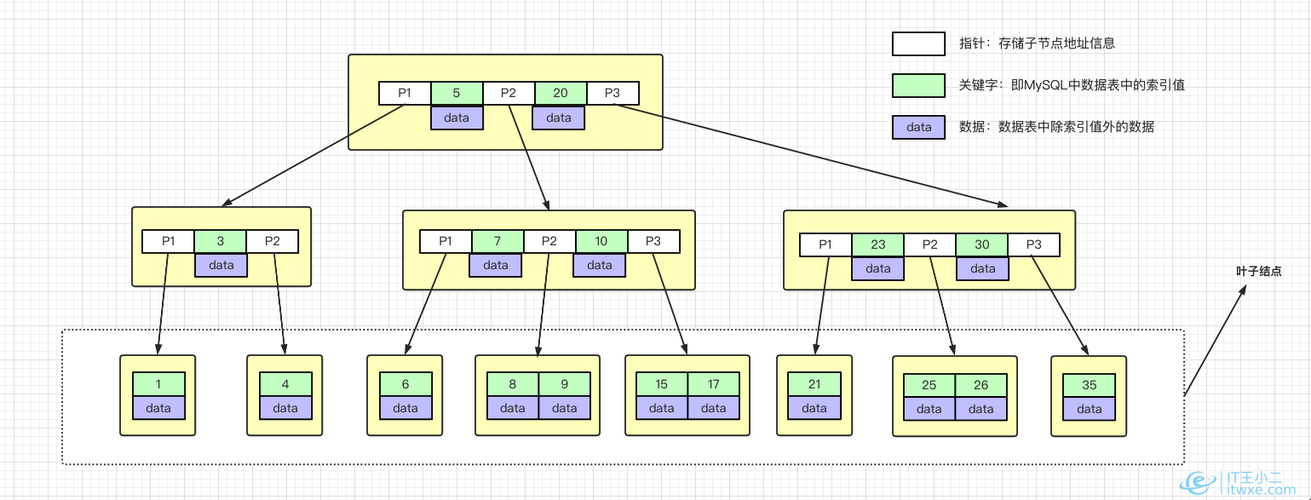
树形构造的关键属性:深度
方案一、毗邻目录模式(adjacency list model)方案事理毗邻目录模式在树形构造数据的每条记录中,记录了指向父数据的记录,如下图所示:

数据库中的表构造如下所示:
id
name
parent
1
上海
中国
2
浦东
上海
查询情形1:当我们须要查询上海的直接父区域时,通过以下Sql查询:
select parent from 区域表 where name = '上海'
查询情形2:当我们须要查询上海的直接子区域时,通过以下Sql查询:
select name from 区域表 where parent = '上海'
查询情形3:当我们须要查询上海的二级子区域时:
select name from 区域表 where parent in (select name from 区域表 where parent = '上海')
查询情形4:当我们须要查询上海的所有子区域,并且不知道区域树的总层数(伪代码):
result_set = select name from 区域表 where parent = '上海';current_parent = select name from 区域表 where parent = '上海';while current_parent is not null:current_parent = select name from 区域表 where parent in current_parentresult_set.add_all(current_parent)
可以看到:此种查询情形下,随着树的高度增加,IO次数也会增加。
方案优缺陷查询所有子树难度:高查询所有父节点难度:高查询下一层子节点难度:低查询上一层父节点难度:低插入新记录的难度:低删除原有记录的难度:低占用额外空间少,只须要占用额外一列O(n)的空间;
适用场景:
只包含直接父子查询的场景包含多层查询,但是可以加载所有数据到内存中的场景方案二、预排序遍历树算法(modified preorder tree traversal algorithm)方案事理预排序的意思便是我们在查询前对存到数据库中的数据进行一次分外的排序,给每条数据添加两个字段:左索引和右索引,添加的办法如下图所示
数据库中的表构造如下所示:
id
name
lindex
rindex
1
上海
16
25
2
浦东
19
24
查询情形1:查找上海有多少子区域(不包含自身):
select rindex-lindex as region_num from 区域表 where name = '上海';
阐明:编号时,可以创造从上海的左侧开始编号递增,回到右侧时候给所有的子节点旁边都编号了一次,以是上海节点的右索引减去左索引除以2(每个子节点有旁边两个编号),便是子节点的总数目。查询情形2:查询上海的所有子区域:
查询情形2:查询上海的所有子区域:
select name from 区域表 where lindex > 16 and rindex < 25;
阐明:由编号过程可以创造,上海子区域的编号值肯定在(19,24)范围内,而非上海子区域的编号范围肯定不在(19,24)范围内,以是此处where中的lindex和rindex可以互换,例如以下语句也可以查询出上海的子区域
select name from 区域表 where lindex > 16 and lindex < 25;
select name from 区域表 where rindex > 16 and rindex < 25;
select name from 区域表 where rindex > 16 and lindex < 25;
查询情形3:查询浦东区域的父区域(上海的父区域只有一个,不直不雅观):
select name from 区域表 where rindex < 19 and lindex > 24;
阐明:由上面的编号过程可知,只要一个节点的旁边编号范围在其余一个节点的旁边编号范围内(查询2的逆推),同理,这个查询语句中的旁边19和24一样可以互换,例如:
select name from 区域表 where rindex < 19 and lindex > 19;
select name from 区域表 where rindex < 24 and lindex > 24;
select name from 区域表 where rindex < 24 and lindex > 19;
修正情形1:删除浦东区域当树形构造变更时,须要重新触发预排序,如删除浦东之后,旁边索引值在19到24的值须要减1,旁边索引大于24的须要减2.
update 区域表 set rindex = rindex-1 where rindex < 24 and rindex > 19;update 区域表 set lindex = lindex-1 where lindex < 24 and lindex > 19;update 区域表 set rindex = rindex-2 where rindex > 24;update 区域表 set lindex = lindex-2 where lindex > 24;
修正情形2:把删除的浦东区域添加回来:
update 区域表 set rindex = rindex+1 where rindex < 24 and rindex >= 19;update 区域表 set lindex = lindex+1 where lindex < 24 and lindex >= 19;update 区域表 set rindex = rindex+2 where rindex >= 24;update 区域表 set lindex = lindex+2 where lindex >= 24;方案优缺陷
查询所有子树难度:低查询所有父节点难度:低查询下一层子节点难度:高查询上一层父节点难度:高插入新记录的难度:高删除原有记录的难度:高占用额外空间少,只须要占用额外一列O(n)的空间;
适用场景:
数据险些不更新的场景。方案三、路径列举法(Path Enumerations)方案事理该方法在每一条数据记录后边添加了一列,用于存储根节点到该点的完全路径。
id
name
path
1
上海
中国/
2
浦东
中国/上海
查询情形1:查找上海有多少子区域(不包含自身):
select name from 区域表 where path like '中国/上海/%';
查询情形2:查询上海区域的所有父区域:
select name from 区域表 where path like '%/上海';
删除/变更/增加情形:删除/变更/增加上海区域:须要更新所有子节点的路径字符串。
方案优缺陷查询所有子树难度:低查询所有父节点难度:低查询下一层子节点难度:低查询上一层父节点难度:低插入新记录的难度:高删除原有记录的难度:高占用额外空间中等,只须要占用额外一列O(n)O(m)的空间(n为节点总数目。m为树的深度);
方案四、ClosureTable方案事理之前的方案中,都是对原有的记录添加列,然后对新增的列进行查询获取父子节点信息关系。而ClosureTable则是新增一张表,用于记录节点直接的关系(父节点,子节点,深度),如下图中的孙桥和浦东,会天生以下关系记录;
id
child
parent
deepth
1
孙桥
浦东
1
2
孙桥
上海
2
3
孙桥
中国
3
4
浦东
上海
1
5
浦东
中国
2
6
上海
中国
1
查询情形1:查询上海的下一层子区域:
select child from 区域表 where parent = '上海' and deepth = 1;
查询情形2:查询上海的所有子区域:
select child from 区域表 where parent = '上海';
查询情形3:查询上海的上一层父区域:
select parent from 区域表 where child = '上海' and deepth = 1;
查询情形4:查询上海的所有父区域:
select parent from 区域表 where child = '上海';
删除情形:删除上海区域:更新上海的子节点的深度:
parents = select parent from 区域表 where child = '上海';children = select child from 区域表 where parent = '上海';update 区域表 set depth = depth -1 where parent in parents and child in children.delete parent from 区域表 where child = '上海' or parent = '上海';方案优缺陷
查询所有子树难度:低查询所有父节点难度:低查询下一层子节点难度:低查询上一层父节点难度:低插入新记录的难度:高删除原有记录的难度:高占用额外空间高,须要额外一张表存O(n)O(m)条记录(n为节点总数目。m为树的深度);
















