贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响往后的状态,只与当前状态有关。
基本要素

编辑
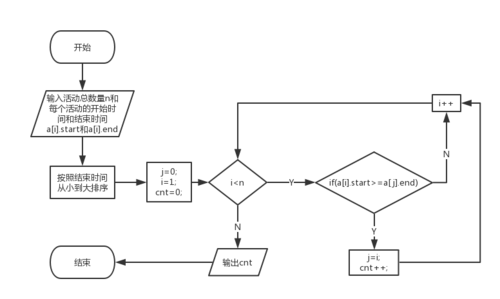
贪心选择
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态方案算法的紧张差异。贪心选择是采取从顶向下、以迭代的方法做出相继选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题。对付一个详细问题,要确定它是否具有贪心选择的性子,我们必须证明每一步所作的贪心选择终极能得到问题的最优解。常日可以首先证明问题的一个整体最优解,是从贪心选择开始的,而且作了贪心选择后,原问题简化为一个规模更小的类似子问题。然后,用数学归纳法证明,通过每一步贪心选择,终极可得到问题的一个整体最优解。
最优子构造
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子构造性子。利用贪心策略在每一次转化时都取得了最优解。问题的最优子构造性子是该问题可用贪心算法或动态方案算法求解的关键特色。贪心算法的每一次操作都对结果产生直接影响,而动态方案则不是。贪心算法对每个子问题的办理方案都做出选择,不能回退;动态方案则会根据以前的选择结果对当提高行选择,有回退功能。动态方案紧张利用于二维或三维问题,而贪心一样平常是一维问题 [2] 。
基本思路
编辑
思想
贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保能得到局部最优解。每一步只考虑一个数据,他的选取该当知足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时,就不把该数据添加到部分解中,直到把所有数据列举完,或者不能再添加算法停滞 [3] 。
过程
建立数学模型来描述问题;把求解的问题分成多少个子问题;对每一子问题求解,得到子问题的局部最优解;把子问题的解局部最优解合本钱来解问题的一个解。算法特性
编辑
贪婪算法可办理的问题常日大部分都有如下的特性:
随着算法的进行,将积累起其它两个凑集:一个包含已经被考虑过并当选出的候选工具,另一个包含已经被考虑过但被丢弃的候选工具。有一个函数来检讨一个候选工具的凑集是否供应了问题的解答。该函数不考虑此时的办理方法是否最优。还有一个函数检讨是否一个候选工具的凑集是可行的,也即是否可能往该凑集上添加更多的候选工具以得到一个解。和上一个函数一样,此时不考虑办理方法的最优性。选择函数可以指出哪一个剩余的候选工具最有希望构成问题的解。末了,目标函数给出解的值。为理解决问题,须要探求一个构成解的候选工具凑集,它可以优化目标函数,贪婪算法一步一步的进行。起初,算法选出的候选工具的凑集为空。接下来的每一步中,根据选择函数,算法从剩余候选工具中选出最有希望构成解的工具。如果凑集中加上该工具后不可行,那么该工具就被丢弃并不再考虑;否则就加到凑集里。每一次都扩充凑集,并检讨该凑集是否构成解。如果贪婪算法精确事情,那么找到的第一个解常日是最优的。例题剖析
编辑
0-1背包问题
有一个背包,背原谅量是M=150kg。有7个物品,物品不可以分割成任意大小。哀求尽可能让装入背包中的物品总代价最大,但不能超过总容量。
物品 A B C D E F G
重量 35kg 30kg 6kg 50kg 40kg 10kg 25kg
代价 10$ 40$ 30$ 50$ 35$ 40$ 30$
剖析:
目标函数:∑pi最大
约束条件是装入的物品总重量不超过背原谅量:∑wi<=M(M=150)
⑴根据贪心的策略,每次挑选代价最大的物品装入背包,得到的结果是否最优?
⑵每次挑选所占重量最小的物品装入是否能得到最优解?
⑶每次选取单位重量代价最大的物品,成为解本题的策略。
值得把稳的是,贪心算法并不是完备不可以利用,贪心策略一旦经由证明成立后,它便是一种高效的算法。
贪心算法还是很常见的算法之一,这是由于它大略易行,布局贪心策略不是很困难。
可惜的是,它须要证明后才能真正利用到题目的算法中。
一样平常来说,贪心算法的证明环绕着:全体问题的最优解一定由在贪心策略中存在的子问题的最优解得来的。
对付例题中的3种贪心策略,都是无法成立(无法被证明)的,阐明如下:
⑴贪心策略:选取代价最大者。
反例:
W=30
物品:A B C
重量:28 12 12
代价:30 20 20
根据策略,首先选取物品A,接下来就无法再选取了,可是,选取B、C则更好。
⑵贪心策略:选取重量最小。它的反例与第一种策略的反例差不多。
⑶贪心策略:选取单位重量代价最大的物品。
反例:
W=30
物品:A B C
重量:28 20 10
代价:28 20 10
根据策略,三种物品单位重量代价一样,程序无法依据现有策略作出判断,如果选择A,则答案缺点。
【把稳:如果物品可以分割为任意大小,那么策略3可得最优解】
对付选取单位重量代价最大的物品这个策略,可以再加一条优化的规则:对付单位重量代价一样的,则优先选择重量小的!
这样,上面的反例就办理了。
但是,如果题目是如下所示,这个策略就也弗成了。
W=40
物品:A B C
重量:25 20 15
代价:25 20 15
附:本题是个DP问题,用贪心法并不一定可以求得最优解,往后理解了动态方案算法后本题就有了新的解法。
马踏棋盘
在8×8方格的棋盘上,从任意指定方格出发,为马探求一条走遍棋盘每一格并且只经由一次的一条路径。
【初步设计】
首先这是一个搜索问题,利用深度优先搜索进行求解。算法如下:
⒈ 输入初始位置坐标x,y;
⒉ 步骤 c:
如果c> 64输出一个解,返回上一步骤c--
(x,y) ← c
打算(x,y)的八个方位的子结点,选出那些可行的子结点
循环遍历所有可行子结点,步骤c++重复2
显然⑵是一个递归调用的过程,大致如下:
C++程序:
#define N 8
void dfs(int x,int y,int count)
{
int i,tx,ty;
if(count>NN)
{
output_solution();//输出一个解
return;
}
for(i=0; i<8; i++)
{
tx=hn[i].x;//hn[]保存八个方位子结点
ty=hn[i].y;
s[tx][ty]=count;
dfs(tx,ty,count+1);//递归调用
s[tx][ty]=0;
}
}
运用
编辑
如把3/7和13/23分别化为三个单位分数的和
【贪心算法】
设a、b为互质正整数,a<b 分数a/b 可用以下的步骤分解成多少个单位分数之和:
步骤一: 用b 除以a,得商数q1 及余数r1。(r1=b - aq1)
步骤二:把a/b 记作:a/b=1/(q1+1)+(a-r1)/b(q1+1)
步骤三:重复步骤2,直到分解完毕
3/7=1/3+2/21=1/3+1/11+1/231
13/23=1/2+3/46=1/2+1/16+1/368
以上实在是数学家斐波那契提出的一种求解埃及分数的贪心算法,准确的算法表述该当是这样的:
设某个真分数的分子为a,分母为b;
把b除以a的商部分加1后的值作为埃及分数的某一个分母c;
将a乘以c再减去b,作为新的a;
将b乘以c,得到新的b;
如果a大于1且能整除b,则末了一个分母为b/a;算法结束;
或者,如果a即是1,则,末了一个分母为b;算法结束;
否则重复上面的步骤。
备注:事实上,后面判断a是否大于1和a是否即是1的两个判断可以合在一起,及判断b%a是否即是0,末了一个分母为b/a,显然是精确的。
PHP代码:
class tanxin{
public $weight;
public $price;
public function __construct($weight=0,$price=0){
$this->weight=$weight;
$this->price=$price;
}
}
//天生数据
$n=10;
for($i=1;$i<=$n;$i++){
$weight=rand(1,20);
$price=rand(1,10);
$x[$i]=new tanxin($weight,$price);
}
//输出结果
function display($x){
$len=count($x);
foreach($x as $val){
echo $val->weight,' ',$val->price;
echo '<br>';
}
}
//按照价格和重量比排序
function tsort(&$x){
$len=count($x);
for($i=1;$i<=$len;$i++)
{
for($j=1;$j<=$len-$i;$j++)
{
$temp=$x[$j];
$res=$x[$j+1]->price/$x[$j+1]->weight;
$temres=$temp->price/$temp->weight;
if($res>$temres){
$x[$j]=$x[$j+1];
$x[$j+1]=$temp;
}
}
}
}
//贪心算法
function tanxin($x,$totalweight=50){
$len=count($x);
$allprice=0;
for($i=1;$i<=$len;$i++){
if($x[$i]->weight>$totalweight) break;
else{
$allprice+=$x[$i]->price;
$totalweight=$totalweight-$x[$i]->weight;
}
}
if($i<$len) $allprice+=$x[$i]->price($totalweight/$x[$i]->weight);
return $allprice;
}
tsort($x);//按非递增次序排序
display($x);//显示
echo '0-1背包最优解为:';
echo tanxin($x);
Java源代码
package main;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
public class Main {
/
测试
/
public static void main(String[] args) {
// 1.随机布局一批任务
List<Pair<Integer>> inputList = new ArrayList<Pair<Integer>>();
Random rand = new Random();
for (int n = 0; n < 20; ++n) {
Integer left = rand.nextInt(100);
Integer right = left + rand.nextInt(100) + 1;
Pair<Integer> pair = new Pair<Integer>(left, right);
inputList.add(pair);
}
// 将任务列表按结束韶光排序(也便是根据right字段进行排序)
sortByRight(inputList);
printPairList(inputList);
// 实行算法
List<Pair<Integer>> outputList = algorithm(inputList);
System.out.println();
printPairList(outputList);
}
/
贪心算法
@paraminputList
@return使数量最多的任务方案
/
public static <T extends Comparable<T>> List<Pair<T>> algorithm(
List<Pair<T>> inputList) {
if (null == inputList || inputList.size() == 0 || inputList.size() == 1) {
return inputList;
}
sortByRight(inputList);
List<Pair<T>> outputList = new ArrayList<Pair<T>>();
int last = 0;
outputList.add(inputList.get(last));
int intputSize = inputList.size();
for (int m = 1; m < intputSize; ++m) {
Pair<T> nextPair = inputList.get(m);
T nextLeft = nextPair.getLeft();
Pair<T> lastOutPair = inputList.get(last);
T lastRight = lastOutPair.getRight();
int flag = nextLeft.compareTo(lastRight);
if (flag >= 0) {
outputList.add(nextPair);
last = m;
}
}
return outputList;
}
/
对传入的List<Pair<T>>工具进行排序,使Pair根据right从小到大排序。
@paraminputList
/
private static <T extends Comparable<T>> void sortByRight(
List<Pair<T>> inputList) {
CompareByRight<T> comparator = new CompareByRight<T>();
Collections.sort(inputList, comparator);
}
/
打印一个List<Pair<T>>工具。
@paraminputList
/
private static <T extends Comparable<T>> void printPairList(
List<Pair<T>> inputList) {
for (Pair<T> pair : inputList) {
System.out.println(pair.toString());
}
}
}
/
根据Pair.right比较两个Pair。用于Conlections.sort()方法。
@param<T>
/
class CompareByRight<T extends Comparable<T>> implements Comparator<Pair<T>> {
/ @ Override /
public int compare(Pair<T> o1, Pair<T> o2) {
T r1 = o1.getRight();
T r2 = o2.getRight();
int flag = r1.compareTo(r2);
return flag;
}
}
/
代表一个任务工具。有点装逼用模板来写了。left表示开始韶光,right表示结束韶光。
@param<T>
/
class Pair<T extends Comparable<T>> {
private T left;
private T right;
public Pair(T left, T right) {
this.left = left;
this.right = right;
}
@Override
public String toString() {
return \"大众[left=\公众 + left.toString() + ',' + \"大众right=\"大众 + right.toString()
+ ']';
}
public T getLeft() {
return left;
}
public void setLeft(T left) {
this.left = left;
}
public T getRight() {
return right;
}
public void setRight(T right) {
this.right = right;
}
















