责编 | 郭芮
出品 | CSDN 博客

scikti-learn 将机器学习分为4个领域,分别是分类(classification)、聚类(clustering)、回归(regression)和降维(dimensionality reduction)。k-means均值算法虽然是聚类算法中比较大略的一种,却包含了丰富的思想内容,非常适宜作为初学者的入门习题。
关于 k-means 均值聚类算法的事理先容、实当代码,网上有很多,但运行效率彷佛都有点问题。本日轻微有点空闲,写了一个不敷20行的 k-means 均值聚类算法,1万个样本均匀耗时20毫秒(10次均值)。同样的数据样本,网优势行的算法均匀耗时3000毫秒(10次均值)。差距竟然达百倍以上,令我深感意外,不由得再次向 numpy 献上膝盖!
以下是我的代码,包含注释、空行统共26行,有效代码16行。
1import numpy as np23def kmeans_xufive(ds, k):4 \"大众\"大众\公众k-means聚类算法56 k - 指定分簇数量7 ds - ndarray(m, n),m个样本的数据集,每个样本n个属性值8 \"大众\"大众\"大众910 m, n = ds.shape # m:样本数量,n:每个样本的属性值个数11 result = np.empty(m, dtype=np.int) # m个样本的聚类结果12 cores = np.empty((k, n)) # k个质心13 cores = ds[np.random.choice(np.arange(m), k, replace=False)] # 从m个数据样本中不重复地随机选择k个样本作为质心1415 while True: # 迭代打算16 d = np.square(np.repeat(ds, k, axis=0).reshape(m, k, n) - cores)17 distance = np.sqrt(np.sum(d, axis=2)) # ndarray(m, k),每个样本间隔k个质心的间隔,共有m行18 index_min = np.argmin(distance, axis=1) # 每个样本间隔最近的质心索引序号1920 if (index_min == result).all: # 如果样本聚类没有改变21 return result, cores # 则返回聚类结果和质心数据2223 result[:] = index_min # 重新分类24 for i in range(k): # 遍历质心集25 items = ds[result==i] # 找出对应该前质心的子样本集26 cores[i] = np.mean(items, axis=0) # 以子样本集的均值作为当前质心的位置
这是网上比较盛行的 k-means 均值聚类算法代码,包含注释、空行统共57行,有效代码37行。
1import numpy as np23# 加载数据4def loadDataSet(fileName):5 data = np.loadtxt(fileName,delimiter='\t')6 return data78# 欧氏间隔打算9 def distEclud(x,y):10 return np.sqrt(np.sum((x-y)2)) # 打算欧氏间隔1112# 为给天命据集构建一个包含K个随机质心的凑集13 def randCent(dataSet,k):14 m,n = dataSet.shape15 centroids = np.zeros((k,n))16 for i in range(k):17 index = int(np.random.uniform(0,m)) #18 centroids[i,:] = dataSet[index,:]19 return centroids2021# k均值聚类22def kmeans_open(dataSet,k):2324 m = np.shape(dataSet)[0] #行的数目25 # 第一列存样本属于哪一簇26 # 第二列存样本的到簇的中央点的偏差27 clusterAssment = np.mat(np.zeros((m,2)))28 clusterChange = True2930 # 第1步 初始化centroids31 centroids = randCent(dataSet,k)32 while clusterChange:33 clusterChange = False3435 # 遍历所有的样本(行数)36 for i in range(m):37 minDist = 100000.038 minIndex = -13940 # 遍历所有的质心41 #第2步 找出最近的质心42 for j in range(k):43 # 打算该样本到质心的欧式间隔44 distance = distEclud(centroids[j,:],dataSet[i,:])45 if distance < minDist:46 minDist = distance47 minIndex = j48 # 第 3 步:更新每一行样本所属的簇49 if clusterAssment[i,0] != minIndex:50 clusterChange = True51 clusterAssment[i,:] = minIndex,minDist252 #第 4 步:更新质心53 for j in range(k):54 pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]] # 获取簇类所有的点55 centroids[j,:] = np.mean(pointsInCluster,axis=0) # 对矩阵的行求均值5657 return clusterAssment.A[:,0], centroids
函数create_data_set,用于天生测试数据。可变参数 cores 是多个三元组,每一个三元组分别是质心的x坐标、y坐标和对该当质心的数据点的数量。
1def create_data_set(cores):2 \"大众\公众\公众天生k-means聚类测试用数据集\"大众\"大众\公众34 ds = list5 for x0, y0, z0 in cores:6 x = np.random.normal(x0, 0.1+np.random.random/3, z0)7 y = np.random.normal(y0, 0.1+np.random.random/3, z0)8 ds.append(np.stack((x,y), axis=1))910 return np.vstack(ds)
测试代码如下:
1import time2import matplotlib.pyplot as plt34k = 45ds = create_data_set((0,0,2500), (0,2,2500), (2,0,2500), (2,2,2500))67t0 = time.time8result, cores = kmeans_xufive(ds, k)9t = time.time - t01011plt.scatter(ds[:,0], ds[:,1], s=1, c=result.astype(np.int))12plt.scatter(cores[:,0], cores[:,1], marker='x', c=np.arange(k))13plt.show1415print(u'利用kmeans_xufive算法,1万个样本点,耗时%f0.3秒'%t)1617t0 = time.time18result, cores = kmeans_open(ds, k)19t = time.time - t02021plt.scatter(ds[:,0], ds[:,1], s=1, c=result.astype(np.int))22plt.scatter(cores[:,0], cores[:,1], marker='x', c=np.arange(k))23plt.show2425print(u'利用kmeans_open算法,1万个样本点,耗时%f0.3秒'%t)
测试结果如下:
1PS D:\XufiveGit\CSDN\code> py -3 .\k-means.py2利用kmeans_xufive算法,1万个样本点,耗时0.0156550.3秒3利用kmeans_open算法,1万个样本点,耗时3.9990890.3秒
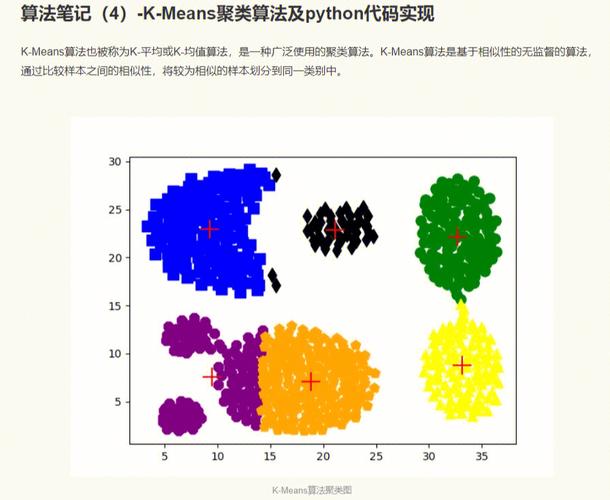
效果如下:
作者:许文武,博客昵称「天元浪子」,本文首发于作者CSDN博客https://blog.csdn.net/xufive/article/details/101448969。
【END】
















