php里面箭号技巧_用Python致敬生命游戏的发明者约翰康威

来源：Freepik ，作者：jcomp

2020年4月11日，普林斯顿大学数学系教授约翰·康威(John Horton Conway)因新冠肺炎去世，终年82岁。

约翰·何顿·康威（John Horton Conway，1937年12月26日－2020年4月11日）

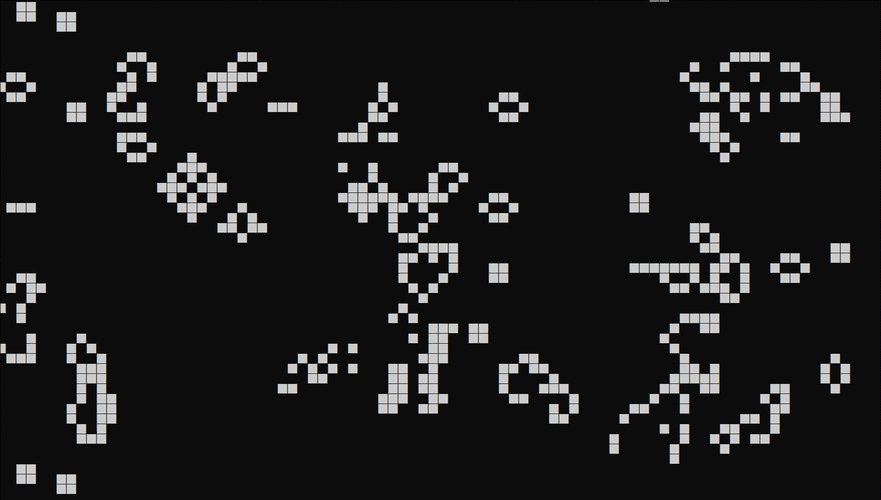
英国皇家学会前主席、数学界的威信人士迈克尔·阿蒂亚（Michael Atiyah）爵士说：

「康威是天下上最神奇的数学家」。

天才数学家陶哲轩写道：

「康威可以说是所有数学家构成的凸包中的extreme point」。

约翰·何顿·康威，1937年生于英国利物浦，数学家，在组合博弈论、有限群的研究、意见意义数学、纽结理论、数论、和编码学等领域都作出过卓越贡献。

在康威浩瀚造诣中，最被众人熟知的莫过于「生命游戏」了。

Conway 生命游戏

「生命游戏」不是一个用来玩的游戏，「生命游戏」实在是「细胞自动机」，即网格上的一组彩色细胞，根据定义相邻细胞状态的一组规则，经由韶光逐步演进。
它的发明者康威称之为「零玩家、永无结局」。

1970年，「生命游戏」的基本规则刊登在《科学美国人》杂志的专栏上，被打算机程序实现后，曾在20世纪70年代风靡一时。

三叶结上的「生命游戏」

高德纳曾做出评论：

「生命游戏」所有规则都是确定性的，但游戏的演进过程却给人一种自主性的觉得。

如今，「生命游戏」既是险些所有学习编程和算法的人都会做到的练习题，也是充满哲理和聪慧的发问——

什么样的生存空间对我们来讲是最得当的？生物个体之间的互动会如何影响到种群的分布和蜕变？

让我们近间隔感想熏染下「生命游戏」是什么，以及如何用Python实现「生命游戏」。
用这种分外的办法，向这位天才数学家致敬。

设定细胞处于ON（活）或OFF（去世）状态，然后为每个细胞分配一个初始状态，由数学规则决定其状态如何随韶光而改变。

Conway「生命游戏」的4个规则：

仿照中的给定细胞(i, j)用二维数组[i][j]来存取，个中 i 和 j 分别是行和列的下标。

生命游戏建立在9个方格的网格中，每个细胞有8个相邻细胞，如图1所示。

在给定时间段，给定细胞的值取决于前一韶光段它的邻居的状态。

图1 8个相邻细胞

在网格边缘的细胞，我们可以采取环形边界条件办理这个问题。

如图2所示，正方形网格先卷起来，使它的水平边缘（A和B）相连，形成一个圆柱体，然后圆柱体的垂直边缘（C和D）相连，以形成一个环面。
形成环面后，所有细胞都有邻居，由于全体空间没有边缘。

图2 环型边界条件的观点视图

这类似于Pac-Man（吃豆子）在边界的事情办法。
如果超出了屏幕的顶部，就会重新在底部涌现。
如果超出了屏幕的左侧，就会重新在右侧涌现。
这种边界条件在二维仿照中很常见。

以下是算法描述：

我们将在Python阐明器中一点一点地仿照编写代码，稽核不同部分所需的代码片段。

用 numpy 数组和 matplotlib 库来显示仿照的输出，用 matplotlib animation 模块更新仿照。

导入该项目利用的模块：

>>> import numpy as np>>> import matplotlib.pyplot as plt>>> import matplotlib.animation as animation表示网格

为了在网格上表示细胞的活（ON）或去世（OFF），分别用 255 和 0 作为 ON 和 OFF 的值。

可以采取 matplotlib 的 imshow() 方法，来显示网格当前的状态，将一个数字矩阵表示为一张图像。

输入以下内容：

❶ >>> x = np.array([[0, 0, 255], [255, 255, 0], [0, 255, 0]])❷ >>> plt.imshow(x, interpolation='nearest') plt.show()

在❶行，定义了3×3的二维numpy数组，数组中的每个元素是一个整数值。

在❷行，用 plt.show() 方法将这个矩阵的值显示为图像，并给 interpolation 选项传入'nearest'值，以得到尖锐的边缘（否则是模糊的）。

图3展示了这段代码的输出。

图3 显示网格的值

把稳，0（OFF）显示为暗灰色，255（ON）显示为浅灰色，这是 imshow() 利用的默认颜色。

要开始仿照，先为二维网格中的每个细胞设置一个初始状态。

若采取随机的初始状态，就利用numpy中random仿照的choice()方法。

输入以下内容：

np.random.choice([0, 255], 44, p=[0.1, 0.9]).reshape(4, 4)

输出：

array([[255, 255, 255, 255], [255, 255, 255, 255], [255, 255, 255, 255], [255, 255, 255, 0]])

np.random.choice从给定的列表[0,255]中选择一个值，每个值涌现的概率由参数p=[0.1, 0.9]指定。
这里，你哀求0涌现的概率是0.1（或10%），255涌现的概率是90%（p中两个值相加必须即是1）。
由于这个choice()方法创建了16个值的一维数组，以是用.reshape使它成为一个二维数组。

若要建立初始条件来匹配特定图案，而不是只填入一组随机值，就将二维网格初始化为零，然后用一个方法在网格的特定行和列增加一个图案，如下所示：

def addGlider(i, j, grid): """adds a glider with top left cell at (i, j)""" ❶ glider = np.array([[0, 0, 255], [255, 0, 255], [0, 255, 255]]) ❷ grid[i:i+3, j:j+3] = glider ❸ grid = np.zeros(NN).reshape(N, N) ❹ addGlider(1, 1, grid)

在❶行，用3×3的numpy数组定义了滑翔机图案（看上去是一种在网格中平稳穿越的图案）。
在❷行，可以看到如何用numpy的切片操作，将这种图案数组复制到仿照的二维网格中，它的左上角放在i和j指定的坐标。
在❸行，创建N×N的零值数组，在❹行，调用addGlider()方法，初始化带有滑翔机图案的网格。

如何实现环形边界条件。

首先，让我们看看在N×N网格的右边缘会发生什么情形。
i行末了一个细胞用grid[i][N-1]来访问。
它右侧的邻居是grid[i][N]，但根据环形边界条件，grid[i][N]访问的值该当由grid[i][0]代替。
下面是一种实现方法：

if j == N-1: right = grid[i][0] else: right = grid[i][j+1]

当然，须要在网格的左侧，顶部和底部运用类似的边界条件，但这样做要加入许多代码，由于须要检测网格的4个边缘。
更简洁的办法是用Python的取模（%）运算符，如下所示：

>>> N = 16 >>> i1 = 14 >>> i2 = 15 >>> (i1+1)%N 15 >>> (i2+1)%N 0

如你所见，%运算符给出整数除以N的余数。
可以用这个运算符让值在边缘折返，像这样重写网格访问代码：

right = grid[i][(j+1)%N]

现在，如果一个细胞在网格边缘（换言之，如果j= N-1），用这种方法要求右边的细胞就会得到(j +1) %N，这将j设回0，让网格右侧卷曲到左侧。
如果在网格底部做同样的事，它就折返到顶部。

生命游戏的规则基于相邻细胞的ON或OFF数目。
为了简化这些规则的运用，可以打算出处于ON状态的相邻细胞总数。
由于ON状态的值为255，以是可以对所有相邻细胞的值求和，再除以255，来得到ON细胞的数量。
下面是干系的代码：

# apply Conway's rules if grid[i, j] == ON: ❶ if (total < 2) or (total > 3): newGrid[i, j] = OFF else: if total == 3: ❷ newGrid[i, j] = ON

在❶行，如果少于2个相邻细胞为ON或多于3个相邻细胞为ON，该细胞就由ON变成OFF。

❷行代码仅适用于OFF细胞：如果恰好有3个相邻细胞为ON，该细胞就变成ON。

下面的代码向程序发送命令行参数：

# main() function def main(): # command line argumentss are in sys.argv[1], sys.argv[2], ... # sys.argv[0] is the script name and can be ignored ❶ # parse arguments parser = argparse.ArgumentParser(description="Runs Conway's Game of Life simulation.") # add arguments ❷ parser.add_argument('--grid-size', dest='N', required=False) ❸ parser.add_argument('--mov-file', dest='movfile', required=False) ❹ parser.add_argument('--interval', dest='interval', required=False) ❺ parser.add_argument('--glider', action='store_true', required=False) args = parser.parse_args()

main()函数首先定义了程序的命令行参数。
在❶行，用argparse类为代码添加命令行选项，然后在接下来几行中添加各种选项。
在❷行，指定仿照网格的大小N。
在❸行，指定保存.mov文件的名称。
在❹行，设置动画更新间隔的毫秒数。
在❺行，用滑翔机图案开始仿照。

接下来一段，对仿照初始化：

# set grid size N = 100 if args.N and int(args.N) > 8: N = int(args.N) # set animation update interval updateInterval = 50 if args.interval: updateInterval = int(args.interval) # declare grid ❶　 grid = np.array([]) # check if "glider" demo flag is specified if args.glider: grid = np.zeros(NN).reshape(N, N) addGlider(1, 1, grid) else: # populate grid with random on/off - more off than on grid = randomGrid(N)

仍在main()函数内，命令行选项解析后，这部分代码运用命令行传入的所有参数。
例如，❶行后的几行设置初始条件，要么是默认的随机图案，要么是滑翔机图案。
末了，设置动画。

# set up the animation ❶　 fig, ax = plt.subplots() img = ax.imshow(grid, interpolation='nearest') ❷　 ani = animation.FuncAnimation(fig, update, fargs=(img, grid, N, ), frames=10, interval=updateInterval, save_count=50) # number of frames? # set the output file if args.movfile: ani.save(args.movfile, fps=30, extra_args=['-vcodec', 'libx264']) plt.show()

在❶行，配置matplotlib的绘图和动画参数。
在❷行，animation.FuncAnimation()调用函数update()，该函数在前面的程序中定义，根据Conway生命游戏的规则，采取环形边界条件来更新网格。

完全程序可从GitHub下载

https://github.com/electronut/pp/blob/master/conway/conway.py

现在运行代码：

$ python3 conway.py

这里采取仿照的默认参数：100×100个细胞的网格，50毫秒的更新间隔。

不雅观看仿照时，你会看到它如何进行，随着韶光的推移创建并保持各种图案，如图4所示。

图4 进行中的生命游戏

图5展示了仿照中可以探求的一些图案。
除了滑翔机，请探求3细胞的闪光灯，以方块或面包的形状等静态图案。

现在，改变一下，用这些参数来运行仿照：

$ python conway.py --grid-size 32 --interval 500 --glider

这里创建了32×32的仿照网格，每500毫秒更新动画，并采取初始的滑翔机图案，如图5所示。

图5 生命游戏中的图案

这里的实现更强调大略，而不是性能。
有许多不同的办法可以加快生命游戏的打算，快速在互联网搜索一下，会创造很多这样的研究。

下面有一些方法，可以进一步试验Conway「生命游戏」。

1．编写addGosperGun()方法，在网格中添加如图6所示的图案。
这种图案被称为“高斯帕滑翔机枪（Gosper Glider Gun）”。
运行仿照并不雅观察枪的行为。

2．编写readPattern()方法，从文本文件读取初始图案，并用它来设置仿照的初始条件。
下面是该文件的建议格式：

8 0 0 0 255 ...

图6 高斯帕滑翔机枪

该文件的第一行定义了N，别的部分是N×N个整数（0或255），由空格隔开。
你可以用Python的方法，如open和file.read来实现。
这种探索有助于研究任何给定的图案在生命游戏规则下是如何演化的。
添加命令行选项--pattern-file，在运行程序时利用此文件。

========

「生命游戏」展现了大略可以如何产生繁芜，就像数学领域乃至全体宇宙一样。

「生命游戏」的算法很大略，但它所提出的问题却发人寻思。
生存空间太大或者太小对发展都是不利的，在一个极度地广人稀的地方，比如在欧美一些地区，O2O的做事，乃至5G通信都不可能发展起来，由于人口的密度太低。

但是，如果人口密度太高，也会存在无限的风险，从这次环球公共卫生事件就能看出来。

「生命游戏」充满了随机性，看似闭幕却也有可能是新的开始，就像康威所说「零玩家、永无结局」。

康威的生平启蒙了万万千万的研究者。
陶哲轩思念道：“我们会记住这样一个有趣的灵魂，我们会怀念这样一个有趣的灵魂！
”

愿他在天国能连续自己的「生命游戏」，永无结局。

以上代码教程部分，节选自《Python极客项目编程》一书，作者：[美] Mahesh Venkitachalam，有编削。

参考文献