phparray查找技巧_轻松掌握二分法查找

二分查找的思想：在一个长度为n的有序数组中查找值即是m的元素位置，先取数组中间位置 mid 的元素与其比较。
如果值即是 m 则返回 mid 值，小于 m 则在数组 0 至 mid-1 区间上按照此方法连续比较查找，大于 m 则在数组 mid + 1 至 n 区间上按照此方法连续比较查找。

假设统共有n个元素，每次查找的区间大小便是n，n/2，n/4，…，n/2^k（操作元素的剩余个数），个中k便是循环的次数。

由于 n/2^k 取整后>=1，即令n/2^k=1

可得k=log2n（因此2为底，n的对数），以是韶光繁芜度表示为O(logn)

二分查找占用空间非常小，额外利用了几个临时变量如left、right、mid，因此其空间繁芜度为O(1)

示例: 从一组有序数组[1,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59]中查询值为37的索引下标

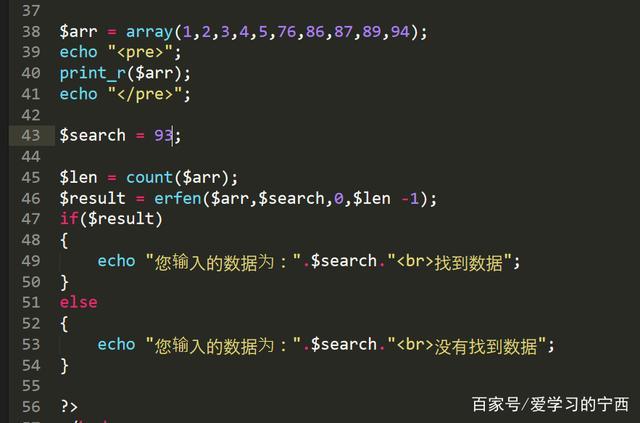
代码实现

二分查找非递归办法代码：

/ 二分查找(非递归办法) @param arr有序数组 @param num 查找元素值 @return boolean /public static int find(int[] arr, int num) {if (arr == null || arr.length == 0) {return -1;}int left = 0;int right = arr.length - 1;while (left <= right) {int mid = (left + right) / 2;if (arr[mid] == num) {return mid;} else if (arr[mid] < num) {left = mid + 1;} else {right = mid - 1;}}return -1;}

二分查找递归办法代码：

/ 二分查找(递归办法) @param arr有序数组 @param num 查找元素值 @return boolean /public static int find(int[] arr, int left, int right, int num) {if (arr == null || arr.length == 0 || left > right) {return -1;}int mid = (left + right) / 2;if (arr[mid] == num) {return mid;} else if (arr[mid] < num) {return find(arr,left + 1, right, num);} else {return find(arr,left + 1, right, num);}}

测试代码：

public static void main(String[] args) {int[] array = new int[] {1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59};System.out.println("二分查找非递归办法: " + find(array, 37));System.out.println("二分查找递归办法: " + find(array, 0, array.length - 1, 37));}

感谢您的阅读，请动动您可爱的小手✌~点赞，留言，关注，分享 4暴击(∩_∩)