来源丨https://zhuanlan.zhihu.com/p/391954665
编辑丨极市平台

最近参加社招,口试基本是问项目,然后问项目里的算法以是这里还是按照实际的口试流程展开总结一下,由于做的项目里面对于不同的领域有一些涉及,以是统一整理一下免得临场忘却,当然,主业还是在machine learning上,以是还是以传统机器学习算法为主,韶光序列预测,nlp,Graph这些涉及的部分只会总结干系的知识点,就不展开来系统性总结了,没啥太大必要也很麻烦.
之前整理的材料紧张是19年10月之前的,这次是整理的险些能找到的所有的19年之后的面经,扩大了范围包括了cv,推举,语音等面经中的知识点,同时增加了那三本面经书的内容一些github上一些比较火的项目,大部分问题是重复的,去重之后实在大概也就百道题的样子.
无监督干系(聚类,非常检测等):问:熟习哪些间隔度量的方法?写一下间隔打算公式?1.连续数据的间隔打算:
闵可夫斯基间隔家族:
当p=1时,便是曼哈顿间隔;
当p=2时,便是欧氏间隔;
当p→∞时,便是切比雪夫间隔。
余弦间隔:
当向量的模长归一化为1时候,余弦间隔和欧式间隔可以相互转换。余弦间隔不是
2.离散数据的间隔打算:
杰卡尔德间隔:A,B凑集的交集/A,B凑集的并集
汉明间隔:表示两个等长字符串在对应位置上不同字符的数目
关于间隔打算,碰着了我在单独研究,由于也是非常大的一块内容。上述的间隔打算公式都是基于样本-样本 之间的大略间隔打算,当引入了查究法进行映射之后还会有一些相应的更繁芜的间隔打算方法,除此之外,迁移学习中的样本群体,即不同数据集之间的分布的间隔的打算也是一大块儿内容,口试的时候该当不会问的太繁芜,这里就暂时不深入展开了。
问:你理解哪些常见的聚类算法?对聚类理解多少?https://zhuanlan.zhihu.com/p/394909171
大略回答,基于划分,基于密度,基于网格,层次聚类,除此之外聚类和其它领域也有很多的结合形成的交叉领域比如半监督聚类,深度聚类,集成聚类等等;
问:kmeans的事理是什么?kmeans是一种基于划分的聚类,中央思想很大略,类内间隔只管即便小,类间间隔只管即便大,算法过程为:
1.初始化k个质心,作为初始的k个簇的中央点,k为人工设定的超参数;
2.所有样本点n分别打算和k个质心的间隔,这里的间隔也是人工定义的可以是不同的间隔打算方法,每个样本点和k个质心中最近的质心划分为1类簇;
3.重新打算质心,方法是针对簇进行聚合打算,kmeans中利用大略均匀的方法进行聚合打算,也可以利用中位数等办法进行打算;
4.重复上述过程直到达到预定的迭代次数或质心不再发生明显变革
问:kmeans的丢失函数是什么?个中,K是聚类数量,p是样本,
是第k个聚类的中央点。SSE越小,解释样本聚合程度越高。
问:kmeans的初始点怎么选择?不同的初始点选择策略有哪些毛病?怎么办理?1.随机初始化:随机选择k个样本点作为初始质心,毛病在于如果选择到的质心间隔很靠近落在同一个簇内,则迭代的结果可能会比较差,由于终极迭代出来的质心点会落在簇间,
最空想的状态是k个质心恰好对应k个簇,由于随机初始化的随机性,可以考虑多次进行随机初始化,选择聚合结果最优的一次(这里涉及到聚类的评估方法);
2.随机分取初始化:即将所有样本点随机授予1个簇的编号,则所有样本点末了会有k个编号,然后进行组均匀,即对付同一个簇的样本进行均匀得到初始化质心。相对付随机初始化,初始的质心会更鲁棒一些,但是仍旧存在随机初始化的毛病,仅仅是缓解;
3.kmeans++
kmeans++是一种启示式的初始化策略:
Kmeans++聚类算法事理与实现:https://zhuanlan.zhihu.com/p/152286357
4.其它聚类算法初始化策略:
利用其它聚类算法打算得到k个质心点作为kmeans的初始质心,我挺懵的,这样彷佛有亿点麻烦。。。
4.kmeans聚的是特色还是样本?特色的间隔如何打算?一样平常情形下是对样本聚类,如果对特色聚类则处理办法也大略,对原始的输入进行.T ,即转置即可。其目的实在和做干系系数类似,如果两个特色高度干系,例如收入和资产水平,则两个特色的间隔相对较小,但是一样平常不可行,由于转置之后,维度每每是非常高的,例如有100万个样本则有100万的维度,打算上不现实,高维数据的间隔度量也是无效的,不如直接打算干系系数;
5.为什么在高维空间中,欧式间隔的度量逐渐失落效?《When Is “Nearest Neighbor” Meaningful?》
维度d趋于无穷大时,高维空间中任意两个样本点的最大间隔和最小间隔趋于相等,间隔度量失落效;
问.怎么确定聚类数量K(聚类如果不清楚有多少类,有什么方法?)和评估分类或回归的办法一样,选择某个metric或某些metrics下最好的k,例如sse(实在便是kmeans的丢失函数了),轮廓系数,兰德指数,互信息等;
如果聚类本身是为了有监督任务做事的(例如聚类产生features用于下贱任务),则可以直接根据下贱任务的metrics进行评估更好;
问:k-means如何调优1.初始化策略调参;
2.k的大小调参,手工方法,手肘法为代表;
3.数据归一化和非常样本的处理;
问:先容一下手肘法(gap statistic的打算很麻烦,这里就不写了)?手肘法实在没什么特殊的,纵轴是聚类效果的评估指标,根据详细的问题而定,如果聚类是作为单独的任务存在则利用sse或轮廓系数这类无监督的metric作为纵坐标,然后找到metric最好并且k最小的结果对应的k为终极的选择;
手肘法实在也很随意马虎做成自动化,我们打算metric变革的斜率就可以了,详细方法便是打算k=n和k=n+1之间的斜率,当 斜率n和斜率n-1,斜率n+1和斜率n,斜率n+2和斜率n+1的差值均小于固定阈值时即可停滞,代码实现上的思路和早停基本是同等的;
问:k-means的缺陷,怎么办理?1.对非常样本很敏感,簇心会由于非常样本被拉得很远
把稳,这里的非常样本指的仅仅是在某些特色维度上取值特殊大或者特殊小的样本,是非常检测中定义的非常样本的一个子集,由于欧式间隔的打算不考虑不同变量之间的联合分布,默认所有特色是相互独立的,以是kmeans中会对结果产生影响的非常样本特指大略的非常样本,即某些特色维度存在非常值的样本,这类非常样本通过大略的统计就可以得到;
办理方法即做好预处理,将非常样本剔除或改动;
2.k值须要事先指定,有时候难以确定;
办理方法即针对k调参;
3.只能拟合球形簇,对付流形簇等不规则的簇或是存在簇重叠问题的繁芜情形等,效果较差
办理方法,换算法;
4.无法处理离散特色,缺失落特色,
5.无法担保全局最优
办理方法:矮子里面挑高个,跑多次,取不同的局部最优里最优的
问:dbscan和optics是怎么办理这些缺陷的?dbscan和optics是基于密度的聚类
1.kmeans对非常样本很敏感,簇心会由于非常样本被拉得很远
dbscan和optics定义了密度的打算办法,不涉及到任何的均匀这种鲁棒性较差的打算办法,对非常样本不敏感,还能检测非常样本呢;
2.k值须要事先指定,有时候难以确定;
dbscan和optics不须要指定簇的数量;算法迭代过程中自然而然产生最优的k个聚类簇;
3.只能拟合球形簇,对付流形簇等不规则的簇或是存在簇重叠问题的繁芜情形等,效果较差
基于密度的聚类可以拟合任意形状的簇,这也归功于密度的打算办法,基于密度的聚类本身不对聚类簇的形状有任何的假设;
4.无法处理离散特色,缺失落特色:缺失落特色要插补,离散特色可以换离散特色的间隔度量方法,基于密度的聚类算法可以灵巧搭配各种不同的distance的度量办法;
5.无法担保全局最优:未办理
问:讲一下dbscan和optics的大致思路?dbscan:单个超球体,病毒式扩散;
optics:两个嵌套的超球体一大一小,先映射为直方图,然后从直方图上天生聚类结果
dbscan和optics:https://zhuanlan.zhihu.com/p/395088759
问:kmeans是否一定可以收敛,为什么?kmeans为什么无法担保全局最优?收敛性证明就算了吧。。.这也太超纲了。.。
kmeans的丢失函数是一个非凸函数,以是无法担保全局最优;
from K Means为什么不能收敛到全局最优点?-SofaSofa:http://sofasofa.io/forum_main_post.php?postid=1002942
kmeans的丢失函数,须要影象一下
这里μk是第k个簇的质心,
为了方便描述,假设x是2维的,取k=1,则我们令:
uk是待求解变量,画出:z=
的函数图像:
可以看到,优化目标z存在(1,1),(-1,1)两个最优解,以是kmeans的丢失函数不是一个凸函数而是一个非凸函数,难以担保收敛到全局最优。
问:为什么在一些场景中要利用余弦相似度而不是欧氏间隔?如果A,B两个向量e 的模场均为1,则欧式间隔和余弦间隔之间知足:
总体来说,欧氏间隔表示数值上的绝对差异,而余弦间隔表示方向上的相对差异。例如,统计两部剧的用户不雅观看行为,用户A的不雅观看向量为(0,1),用户B为 (1,0);此时二者的余弦间隔很大,而欧氏间隔很小;我们剖析两个用户对付不同视频的偏好,更关注相对差异,显然应该利用余弦间隔。而当我们剖析用户生动度,以上岸次数(单位:次)和均匀不雅观看时长(单位:分钟)作为特色时,余弦间隔会认为(1,10)、(10,100)两个用户间隔很近;但显然这两个用户生动度是有着极大差异的。
因此,我们关注向量数值绝对差异,应该利用欧氏间隔,如果关心的是向量方向上的相对差异,则应该利用余弦间隔。
问:余弦间隔是否是一个严格定义的间隔? (一个度量标准要知足什么哀求才能算是间隔)该题紧张稽核口试者对间隔的定义的理解,以及大略的反证和推导。首先看 间隔的定义:在一个凑集中,如果每一对元素均可唯一确定一个实数,使得三条间隔公理(正定性,对称性,三角不等式)成立,则该实数可称为这对元素之间的间隔。
余弦间隔知足正定性和对称性,但是不知足三角不等式,因此它并不是严格定义的间隔。
问:K-means 中我想聚成100类 结果创造只能聚成98类,为什么?迭代的过程中涌现空簇,缘故原由在于k太大,实际的簇数量小于k;
初始化策略不会导致空簇的问题,由于纵然最大略的随机初始化也是从原始的样本点里选择部分样本作为质心,如果初始质心中存在非常样本,则终极聚类的结果,这个非常点会自成一个簇而不会涌现空簇的问题;
https://datascience.stackexchange.com/questions/44897/k-means-clustering-what-to-do-if-a-cluster-has-0-elements
空簇对应的中央点和任意一个样本点的间隔都不是该样本点间隔其它质心点的间隔的最小值。
问:kmeans,GMM,EM之间有什么关系?kmeans是基于划分的聚类算法,GMM是基于模型的聚类算法,EM是估计GMM的参数利用的优化算法;
1. kmeans可以看作是GMM的一种特例,于协方差为单位矩阵,故kmeans聚类的形状是球形的,而GMM是椭球型的;
2. kmeans利用hard EM求解,GMM利用soft EM求解(kmeans觉得还是从直不雅观上的打算过程上理解比较舒畅,通过hard em也是一个阐明便是了);
关于上述的缘故原由,不才一个问题里解释
问:高斯稠浊模型的核心思想是什么?(GMM和多元高斯有什么差异?,多元高斯函数的期望是什么)GMM便是多个干系多元高斯分布的加权求和;
理解GMM之前,先回归基本观点:
1.一元高斯分布:
现在我们将高斯分布扩展到多维空间,大略说便是有x1,x2,x3。。。xn等多个维度。当我们假设多维空间的每一个空间之间完备独立,则独立的n元高斯分布为:
可以看到,是非常类似的,根号2pi部分取n次方,方差用协方差矩阵代替,代数的乘法转化为矩阵乘法;多元高斯分布的期望便是不雅观测样本的(样本向量-所有特色向量的均值构成的均值向量)进行和自身的向量乘打算;
协方差矩阵:
协方差矩阵是一个nXn的矩阵,n代表了多元的大小,对付协方差矩阵中的每一个元素,打算公式如下:
详细展开来看便是:
协方差矩阵和干系系数的关系:
可以看到,干系系数的打算过程中,已经对变量做了均值方差的标准化处理了,以是对两个特色打算干系系数不须要考虑量纲大小的问题;
现实天下中,不同的特色(多个特色=多元)很难完备独立,因此我们也会利用非独立的多元高斯分布,公式写作:
可以看到,公式层面上,独立多元高斯分布和非独立(干系)多元高斯分布的形式是一样的,只不过协方差矩阵不同:
独立多元高斯分布除对角线之外其它元素的值均为0,干系多元高斯分布则其它元素的值为特色之间的协方差的打算结果;
高斯稠浊模型:
高斯稠浊模型GMM是多元高斯分布之上的观点,他认为现实天下的数据是由多个不同参数的干系多元高斯模型以不同的权重累积求和构成的(单元,独立多元高斯模型可以看作干系多元高斯模型的特例);
个中:
对付干系多元高斯稠浊模型,其参数仅包含均值向量和协方差矩阵,可以直接通过极大似然法写出极大似然函数,然后通过求导进行参数估计,详细的通过极大似然法可以直接推导出均值向量和协方差矩阵关于输入向量X的打算公式,带入数据集X可以直接求解;
而GMM的极大似然函数较为繁芜:
问:GMM是如何迭代打算的?为什么kmeans,GMM,EM知足上面描述的办法?(EM算法数学事理)
首先须要理解em算法,em算法和梯度低落法一样,都可以用来优化极大似然函数,当极大似然函数中存在隐变量时,EM算法是一种常用的优化算法;
EM算法是一种迭代优化策略,由于它的打算方法中每一次迭代都分两步,个中一个为期望步(E步),另一个为极大步(M步),以是EM算法被称为EM算法(Expectation-Maximization Algorithm)
jensen不等式:
如上图,实线f表示凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。X的期望值便是a和b的中值,从图中可以看到成立。
问:GMM的丢失函数?增大数据量是否会更好?问:层次聚类事理问:为什么选择伶仃森林?先容一下iforest?优点:基于集成非常检测的思路,鲁棒性强;不涉及间隔和密度打算,打算速率很快;每棵树独立天生可并行或分布式;
iforest的算法流程:
(1)底层是极限随机树,随机选择一个特色,随机选择部分样本(bagging),每次分裂随机选择一个分裂节点,最大深度是 log2(bagging的样本数量)
(2)整合所有极限随机树的结果,利用score function打分:
h(x) 为 样本x 在每棵树的高度(实在便是x在这棵树上分裂了几次),对样本x在所有树上的分裂次数进行均匀得到分子项目,c(Ψ) 为给定样本数 Ψ 时路径长度的均匀值,用来对样本 x 的路径长度 h(x) 进行标准化处理。
(3)score function的打算结果在0~1之间,
如果非常得分靠近 1,那么一定是非常点;
如果非常得分远小于 0.5,那么一定不是非常点;
如果非常得分所有点的得分都在 0.5 旁边,那么样本中很可能不存在非常点。
详细的可见:
isolation forest:https://zhuanlan.zhihu.com/p/181378482
isolation forest的score function公式到底是个啥?:https://zhuanlan.zhihu.com/p/181650438
追问:为什么高度为log2(bagging的样本数量)?为什么每次随机仅选择一小部分的样本(默认是min(bagging的样本数量,256))?直不雅观上来看,m个特色,我们用m个极限随机树分别进行完备分裂,分裂到叶子节点的样本特色值完备相同,得到n个样本在m个极限随机树上的分裂次数,即得到n个样本在m个特色上的分裂次数,然后取均匀就可以知足我们的预测目标了。实质上通过分裂次数代替聚类或密度的打算,分裂越少,则样本在这个特色上的非常程度越高,然后综合考虑样本在多个特色上的非常程度;
但是这么做的问题有:
1.打算繁芜度太高了,树的完备分裂的韶光繁芜度为O(n),上述做法的总的韶光繁芜度为O(mn);
2.实质上做的是基于集成学习的无监督学习,鲁棒性强,但是纯挚用1个极限随机树分裂1个特色,随机成分影响太大,重新演习的结果差异可能会很大。办理的方法是每个特色用多个极限随机树来拟合,则打算繁芜度进一步扩大为O(mnk),k为树的数量;
3.无监督的核心毛病,无法自动特色选择,所有特色的主要性等量齐观,则如果存在大量无用特色或者噪声特色,会严重影响打算结果;
iforest针对上述问题做了改进:
1.针对问题1,树的最大深度限定为log2(bagging的样本数量),之以是对树的高度做限定,是由于我们只关心路径长度较短的点,它们更可能是非常点,而并不关心那些路径很长的正常点。之以是利用log2的底数,是为了和score function的公式对应起来,为了打算score fuction上的便利性:
2-log2(2)=1/2,2log2(2)=2(指数和log打算公式)
总结一下, log2(bagging的样本数量)和做事于score function的设计的,打算上供应了便利性,;
2.仍旧是针对问题1,树每次利用的样本默认为 min(采样的样本数,256),这么做紧张避免了太大数量的样本上分裂次数过多打算繁芜度高的问题,然后通过集成提高全体模型的鲁棒性。(精度和效率之间的一种折衷,根据论文和实际的运用结果,效果还ok);
3.针对问题2,仍旧是精度和效率上的折衷,k个极限随机树通过采样,终极一共利用k个特色,每一轮随机选择一个特色天生一棵树;
4.针对问题1和2的禁绝确分裂的问题(本色上也没有办法做精确分裂),tree分裂上的禁绝确在实践中可以被认为提高了算法的鲁棒性,类似于lgb直方图;
5.针对问题3,特色的随机采样某些情形下缓解了无效特色的问题(大部分特色有效少部分特色无效的情形),但是实质上没有办理(大部分特色无效,少部分特色有效的情形),终极的特色工程还是要基于业务履历来进行;
追问:iforest的score function,为什么这么设计?一步一步拆解来看:
1.指数函数形式的设计
我们希望iforest输出的结果能够在一个有限的范围内,例如像auc的取值范围为0.5~1一样平常,有界的评估指标便于比较(高度一定为正数,因此分子部分可以担保为负数,2-x一定是大于0小于1的);
2.分子的设计:
h(x)部分,并不是大略的直接打算样本在tree上的分裂次数,不雅观察上述公式,个中e表示的才是样本在tree上的分裂次数,后面额外多了一项c(T.size)的改动项,T.size表示的样当地点叶子节点中所有样本的数量。
c(n)表示样本数量为n的情形下,天生随机二叉树的期望高度:
3.分母部分的设计:
分母部分利用的仍旧是上述的C(n)的公式,只不过分母部分的n指的是每一棵极限随机树利用的全部样本数量,即bagging得到的样本数量,默认是256个样本。这里的分母也是作为改动项存在的。
追问:为什么这里要引入分子和分母部分的改动项?1.分子部分的改动项:
紧张目的在于将样本落在的叶子节点中的样本数量大小这一成分考虑进来,假设某个样本A落入了叶子节点1,叶子节点1中有5个样本;某个样本B落入了叶子节点2,叶子节点2中有5000个样本,并且假设A和B的树的深度e都是3,则如果我们不引入改动项c(T.size),打算结果是完备相同的。但实际上很明显,A的非常程度是要高于B的,由于B所在的叶子节点的样本数量很大,实在是可以连续分裂很多次,然而考虑到性能的问题,我们对树的高度做了限定,因此会引发这样的偏差。
改动项的引入可以很好的办理这个问题 ,C(n)代表了给定n个叶子节点,所能天生的随机二叉树的均匀高度,显然,叶子节点数量越多,则均匀高度越大,则score function的打算结果越小,从而奥妙地缓解了上述存在的问题;
2.分母部分的改动项:
紧张目的在于将每个tree所演习的bagging的样本数大小这一成分考虑进来,假设bagging的样今年夜小为64和256,则根据iforest的设计,max_depth分别为5和8,显然,bagging的样本数量越大则树可以天生的树的深度大概率越深,因此在分母部分引入给定bagging样本数量下,所能天生的随机二叉树的均匀高度,显然,bagging样本数越多,均匀高度越大,则score function打算的结果越大。
问:KNN算法是否存在丢失函数?无,knn是一种
lazy learning:
只存储数据集而不从中学习,不须要模型演习收到测试数据后开始根据存储数据集对数据进行分类或回归;eager learning:
1.从网络到的数据中学习,须要模型演习;
2.受到测试数据后直接完身分类或回归
不屈衡学习:问:数据不屈衡如何办理,抽样得到的分类准确率如何转换为原准确率?将采样后的预测的种别按照采样比例进行相应的增大或减少,例如对种别A下采样了50%,则预测结果中种别A的预测数量为m,令m=m/0.5=2m,然后打算分类准确率;
这种处理办法是不准确的,合理的办法该当是直接对原始数据进行评估指标的打算;
问:办理难样本问题的方法(hard sample problem),ohem与focal loss的相同点和不同点
问:如果把不平衡的演习集(正负样本1:3)通过降采样平衡后,那么对付平衡后的AUC值和预测概率值有若何的变革?roc曲线对种别数量的变革不敏感,因此auc的打算结果整体不会发生明显变革;
通过下采样平衡后,变相增大了正样本数量,分类决策边界阔别正样本,预测概率整体变大;
问:class_weight的思想是什么?class_weight对应的大略加权法是代价敏感学习最大略的一种方法,思想便是小类样本加权,使其在loss中比重变大;
问:不屈衡学习事理?目前主流的不屈衡学习紧张是关于分类问题的不屈衡。所谓不屈衡分类,指的是样天职歧类别的数量差异越来越大的情形下,模型越来越倾向于预测大类样本的征象,因此,模型分类性能越来越差。
纯挚从样本不屈衡的角度出发(不考虑分布变革,小样本学习,分类问题的困难程度等其它问题),不屈衡的种别对模型造成影响的缘故原由:
1.目标函数优化的方法,利用梯度低落法优化目标函数的模型对付不屈衡问题更敏感;而tree模型纯粹基于贪心策略进行分裂的方法则对此并不敏感;
2.目标函数的利用,hinge loss和交叉熵对付不屈衡的敏感度不同;
不屈衡是一个征象,是分类模型效果差的潜在缘故原由之一;
问:理解哪些不屈衡学习的处理方法?讲讲smote算法的事理?为什么平常很少利用smote这类基于样本天生的方法?问:过采样(上采样)和天生样本的差异?上采样不一定是天生样本,例如大略的repeat式的上采样,通过repeat不涉及样本天生的过程,但天生样本一定是一种上采样;
模型的loss function,metrics和optimizers无监督metrics:问:如何评价聚类结果的好坏(知道哪些聚类的评估指标)?轮廓系数有没有用过sse很大略
轮廓系数:
轮廓系数是为每个样本定义的,由两个分数组成:
a:样本与同一cluster中所有其他点之间的均匀间隔。b:样本与_下一个最近cluster_中的所有其他点之间的均匀间隔。对付单个样本而言,轮廓系数的打算公式如下:
对付模型评估而言,取所有样本的轮廓系数的均值作为模型聚类效果的评估指标;
其它评估办法可见:
https://scikit-learn.org/stable/modules/clustering.html#clustering-performance-evaluation
有监督metrics:问:准确率的局限性是什么?1.不同分类阈值下准确率会发生变革,评估起来比较麻烦;
2.对样本不屈衡问题特殊敏感,例如当负样本占99%时,分类器把所有样本都预测为负样本也可以得到99%的准确率;
公式: 分类精确的样本数/总样本数
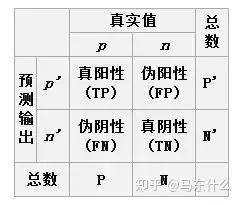
问:ROC曲线如何绘制,ROC和PRC的异同点;准确率(accuracy)、精确率(precision)、召回率(recall),各自的定义,各自的毛病;PR曲线的绘制;利用PR曲线判断模型好坏;ROC曲线的横坐标、纵坐标意义;TP,FP,TN,FN,都是英文缩写很好影象
准确率=(tp+tn)/total
精确率=tp/(tp+fp) 分子为精确预测的正样本的样本数量,分母为预测为正样本的样本数量
召回率=tp/(tp+fn) 分子为精确预测的正样本的样本数量,分母为所有正样本的样本数量
误杀率=fp/(fp+tn) 分子为缺点预测的正样本数量,分母为所有负样本的样本数量
极度不屈衡情形下,模型将所有样本预测为大类则准确率就能很高了;
分类阈值靠近0,则模型将所有样本预测为正样本则召回率靠近100%;
分类阈值靠近1,则模型将极少样本预测为正样本则精确率靠近100%(例如就预测一个样本为正样本并且这个样本恰好为正样本则精确率为1);
召回和精确率都受到分类阈值的影响较大;
pr曲线,以召回率为横坐标,精确率为纵坐标
如果一个学习器的P-R曲线被另一个学习器的P-R曲线完备包住,则可认为后者的性能优于前者,例如上面的A和B优于学习器C;
一样平常利用平衡点来评估无法直接比较的情形例如上图的A和B模型,平衡点(BEP)是P=R时的取值,如果这个值较大,则解释学习器的性能较好。而F1 = 2 召回率 精确率 /( 召回率 + 精确率 ),同样,F1值越大,我们可以认为该学习器的性能较好。
roc曲线,和pr曲线一样,纵坐标是精确率,但是横坐标是误杀率。
个中第一行ab均为原数据的图,左边为ROC曲线,右边为P-R曲线。第二行cd为负样本增大10倍后俩个曲线的图。可以看出,ROC曲线基本没有变革,但P-R曲线确剧烈震荡。因此,在面对正负样本数量非常不屈衡的场景下,ROC曲线会是一个更加稳定能反响模型好坏的指标,
问:ROC曲线和PR曲线的差异,适用场景,各自优缺陷;roc曲线对付正负样本比例不敏感,由于roc曲线的纵坐标是精确率=预测精确的正样本/预测为正样本的样本数量,横坐标是误杀率=预测缺点的负样本/所有负样本数量,改变了标签中类别的分布之后,预测精确的正样本/预测为正样本的样本数量 会同时发生同向的变革,预测缺点的负样本/所有负样本数量 也会发生同向的变革,即roc的横纵坐标的打算结果是独立的,分别是针对正样本和针对负样本独立打算的,两个坐标的打算不会发生相互影响,因此种别比例发生变革的情形下,roc也不会产生剧烈的变动;
pr曲线的纵坐标是精确率=预测精确的正样本/预测为正样本的样本数量,横坐标是召回率=预测精确的正样本/所有正样本的数量,即pr的横纵坐标的打算结果是存在相互关系的,他们都是针对正样本进行打算,两个坐标的打算发生相互影响,从而使得pr曲线对类别的变革很敏感;
roc聚焦于二分类模型整体对正负样本的预测能力,以是适用于评估模型整体的性能;如果紧张关注正样本的预测能力而不care负样本的预测能力,则pr曲线更得当;
问:AUC的意义,AUC的打算公式?auc是roc的曲线下面积,但是auc的实际意义仅仅从roc的曲线下面积不好理解,这里可以先理解一下auc的打算公式有哪些:
直接根据roc曲线进行打算,打算roc曲线下面积,缺陷是打算偏差较大,我们须要确定非常大量的分类阈值才能毕竟auc的真实打算结果;
2.auc的实际意义:正负样本对中预测结果的rank值的比较,假设正样本有x1个,负样本有x0个,则统计正样本负样本的样本对中,正样本的预测概率大于负样本的预测概率的样本数量z,然后用z/x0x1就可以得到auc了,这种打算办法的韶光繁芜度为O(n^2),这里的n指的是样本总数量
3.在2的根本上改进,先对预测的结果进行rank,预测概率越大则rank值越大,
这里的公式写的比较简单,详细阐明一下:
首先, 假设某个样本 S 的rank值为k,则意味着有k-1个样本的预测概率小于样本S,即对付这k-1个样本中的每一个样本s来说,他们分别和样本S 构成的 sample pair (S,s)都是S的rank大而s的rank小的 ,则我们可以先得到:
然后, 对付M个正样本而言,两个正样本构成的pair是没故意义的,我们在2里的打算不涉及到正样本之间的匹配,因此这部分须要减掉,则M个正样本两两配对的组合数量为
末了, 对付rank值而言,例如样本S的rank值为10,则实际上是有9个样本的预测值小于样本S的,但是我们前面的求和部分实际年夜将样本S和自身的sample pair(S,S)都考虑进去了,以是这里减掉和自身匹配的情形,一共是M种;
终极,我们就得到了:
韶光繁芜度取决于利用了排序算法,利用快排则打算繁芜度为O(nlog(n))
因此,auc的实际意义是任意选定一个正负样本对,正样本的预测结果大于负样本的预测结果的概率;
问:给你M个正样本,N个负样本,以及他们的预测值P,求AUC预测值取rank然后套上面公式就行了;
问:IV值,woe值是什么?woe是一种用于种别特色编码的编码方法,公式为:
大略来说,便是某个类别的好坏比/全量数据的好坏比;
iv是对woe值的改动,紧张是考虑种别中包含的样本数量大小不同从而导致相同woe打算结果下,统计特色不明显的问题,不同样本数量下打算出来的woe是具有不同意义的,大略来说,woe打算结果相同的情形下,种别中包含的样本数量越多,woe的显著性越明显;
woe由于存在上述的问题,以是从全体特色的层面来看不能直接求和,但iv可以
问:roc曲线中,高于和低于对角线表示意义
roc曲线的对角线,表示一个随机预测模型的性能,如果模型的roc曲线在对角线下方,则该模型比随机模型还差,高于对角线则表示模型比随机模型好,模型是故意义的;
详细的,可以从auc的物理意义上去理解,roc的对角线下方面积为0.5,意味着对角线的随机模型的auc为0.5,结合auc的物理意义:任意选择一个正负样本对,正样本的预测结果高于负样本的预测结果的概率,则解释对角线代表的随机模型对付正负样本对的相对大小的剖断是随机的;
问:多分类 auc 怎么算?多分类问题中,在二分类指标的根本上须要进行一些处理才能适配多分类的评估,整体有两种打算策略:
基于macro的策略:ovr的划分办法,分别打算每个类别的metrics然后再进行均匀
基于micro的策略:所有类放在一起算metrics;
micro的评估办法,当种别非常不屈衡时,micro的打算结果会被样本数量多的种别主导,此时须要利用macro
问:F1,F2.。。.Fn值是什么,Fbeta怎么打算?fbeta是f_metrics系列的终极定义式,公式如下:(f系列的可以统一用这个公式来影象)
当beta=1时,Fbeta=F1,当beta=n时,Fbeta=fn;
beta用于定义召回率和精确率的相对主要性,越大,则recall越主要,当beta趋于无穷大时,Fbeta=recall,越小,则precision越主要,当beta2趋于0时,Fbeta=precision
问:ks曲线和psi理解吗?ks曲线的横坐标是分类的阈值,纵坐标代表了精确率或者误杀率,一个分类阈值对应的一个精确率和一个误杀率,而ks曲线便是用每个分类阈值下的精确率-误杀率,ks值则是指ks曲线上的最大值;
psi:
psi便是对称的kl散度的均匀,kl散度的公式如下:
用来衡量两个离散随机变量的分布的差异
loss function问:知道哪些常见的丢失函数?点预测问题:
0-1丢失函数:
非凸,直接优化困难
logloss(交叉熵)(多分类),
最常用,相对hinge loss对噪声敏感(无意义的hard sample);
Cross-entropy(二元交叉熵)(logloss在二分类的特例):
当利用sigmoid作为激活函数的时候,常用交叉熵丢失函数而不用均方偏差丢失函数,由于它可以完美办理平方丢失函数权重更新过慢的问题,具有“偏差大的时候,权重更新快;偏差小的时候,权重更新慢”的良好性子。
exponential loss
对噪声敏感,adaboost中利用过,其它情形很少打仗
hingeloss,
对噪声健壮性强;
mse,mae,rmse,mape,smape:
mse,mae,rmse对标签y取值特殊大的样本鲁棒性都较差,mae和rmse相对有所缓解,
mape:范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型。
可以看到,MAPE便是mae 多了个分母。
把稳点:当真实值有数据即是0时,存在分母0除问题,须要做平滑
mape对标签y取值特殊大的样本的鲁棒性较强,由于通过除以真实标签(即分母项),对单个非常样本的loss进行了放缩;毛病在于对标签y取值靠近0的样本鲁棒性很差,一点点的偏差就会使得单个样本的mape的loss的打算结果很大,
smape:smape是针对mape的对非常小样本的鲁棒性很差的问题进行了改动,可以较好的避免mape由于真实值yi小而打算结果太大的问题;同时对非常大的样本的鲁棒性也较好;
mape和smape都可以作为loss function进行优化;
区间预测问题:
直接估计参数的分布的参数,贝叶斯深度学习这部分内容里有,之前看的deepar也是用的这种,称为distribution loss,这块儿研究的不多,后续该当找个韶光好好系统性的看一下回归中的区间预测问题;
问:mse对付非常样本的鲁棒性差的问题怎么办理?1、如果非常样本无意义,则对非常样本进行平滑等办法处理成正常样本,如果非常样本很稀少,直接删除也可以;
2. 如果非常样本故意义,例如双十一销量,须要模型把这些故意义的非常考虑进来,则从模型侧考虑利用表达能力更强的模型或复合模型或分群建模等;
3.loss function层面选择更鲁棒的丢失函数例如smape;
问:二分类为什么用二元交叉熵?为什么不用mse?缘故原由:sigmoid对模型输出进行压缩到(0,1)区间的条件下,根据二元交叉熵得到的梯度更新公式中不包含sigmoid的求导项,根据mse的得到的梯度更新公式则会包含。
利用mse推导出的梯度更新量:
根据二元交叉熵推导出来的梯度更新公式:
不包含sigmoid的求导项,没这个问题
问:mse,sigmoid+交叉熵梯度推导mse
没有sigmoid或其它的转换,则公式中求导项为1,
二元交叉熵(带sigmoid,求导过程中用到sigmoid的导数公式,否则到第二张图的第二步就可以停滞了):
问:信息量,信息熵、相对熵(KL散度)、交叉熵、条件熵、互信息、联合熵的观点和公式?信息量用来度量一个事宜的不愿定性程度,不愿定性越高则信息量越大,一样平常通过事宜发生的概率来定义不愿定性,信息量则是基于概率密度函数的log运算,用以下式子定义:
这里的p(x)可以是离散数据的概率,也可以是连续数据的概率密度函数
信息熵,衡量的是一个事宜凑集的不愿定性程度,便是事宜凑集中所有事宜的不愿定性的期望,公式定义如下:
相对熵(kl散度):kl散度,从概统角度出发,表示用于两个概率分布的差异的非对称衡量,kl散度也可以从信息理论的角度出发,从这个角度出发的kl散度我们也可以称之为相对熵,实际上描述的是两个概率分布的信息熵的差值:
对付离散和连续的随机变量分布都可以利用kl散度进行定义
kl散度和余弦间隔一样,不知足间隔的严格定义;
kl散度的性子:
非负性(用Jenson‘s inequality 证明)不对称性,即KL(P||Q)≠KL(Q||P)js散度公式如下:
js散度的范围是[0,1],相同则是0,相反为1。相较于KL,对相似度的判别更准确;同时,js散度知足对称性 JS(P||Q)=JS(Q||P)
交叉熵:
可见,交叉熵便是真值分布的信息熵与KL散度的和, 而真值的熵是确定的,与模型的参数θ 无关,以是梯度低落求导时,优化交叉熵和优化kl散度(相对熵)是一样的;
联合熵:
联合熵实际上衡量的是两个事宜凑集,经由组合之后形成的新的大的事宜凑集的信息熵;
条件熵:
事宜凑集Y的条件熵=联合熵-事宜凑集X的信息熵,用来衡量在事宜凑集X已知的根本上,事宜凑集Y的不愿定性的减少程度;
互信息:
互信息=事宜凑集X的信息熵-事宜凑集X在已知事宜凑集Y下的条件熵=事宜集Y的信息熵-事宜凑集Y在已知事宜凑集X下的条件熵;
问:怎么衡量两个分布的差异?KL散度和交叉熵丢失有什么不同?关系是啥?kl散度,js散度,以及迁移学习里的许多更advanced的评估办法例如mmd,交叉熵=真实的标签分布的信息熵+相对熵(kl散度)
问:间隔的定义?哪些度量方法不符合间隔的定义间隔的定义:在一个凑集中,如果每一对元素均可唯一确定一个实数,使得三条间隔公理(正定性,对称性,三角不等式)成立,则该实数可称为这对元素之间的间隔。
1:正定性,d(x,y)>=0,仅当x=y则不等式等号成立,说白了便是如果样本A和样本B的间隔为0,则样本A和样本B可以看作同一个样本;
2:对称性:d(x,y)=d(y,x),即样本A到样本B的间隔即是样本B到样本A的间隔;
3:d(x,y)<d(x,z)+d(z,y),即样本A到样本B的间隔小于样本A到样本C的间隔+样本B到样本C的间隔
余弦间隔不知足三角不等式,kl散度不知足对称性,因此二者都不是严格意义上的间隔的定义;
问:交叉熵的设计思想是什么?优化交叉熵等价于优化kl散度,
问:写 huber loss 公式,huber loss理解吗?和mse、比起来上风是啥?通过引入超参数sigma,huber loss可以灵巧动态的调度模型利用的loss function是mse还是mae,
这确保了丢失函数不会受到非常值的严重影响,同时不会完备忽略它们的影响。
最优化方法:问:推导梯度低落公式这里问的是梯度低落的一样平常性的表达式:
不知道这种问题有什么好问的。。
问:知道哪些常见的一、二阶优化方法?牛顿法的收敛速率,是不是一定比梯度低落快(举反例),Hessian矩阵的求逆与打算量问题(正则化,Hessian矩阵的近似),牛顿低落的几个phase,KKT的仔细描述。拟牛顿法和牛顿法的关系,拟牛顿法办理了牛顿法哪个问题?推导下牛顿法。牛顿法在什么时候只须要迭代一次就能求解,什么时候牛顿法不能适用
问:极大似然估计,构造,履历风险最小化的关系,交叉熵和最大似然 丢失函数的差异,讲一下极大似然估计,极大似然估计和最大后验估计的差异是什么?最小二乘与极大似然函数的关系?先验,后验,最大似然估计,最大后验估计?问:讲一下jaccob矩阵和Hessian矩阵?Hessian矩阵是对称矩阵吗?问: 机器学习中的优化问题,哪些是凸优化问题,哪些是非凸优化问题?请各举 一个例子。凸函数的严格定义为,函数_L_(·) 是凸函数当且仅当对定义域中的任意两点_x_,_y_和任意实数_λ_∈[0,1]总有
该不等式的一个直不雅观阐明是,凸函数曲面上任意两点连接而成的线段,其上的任 意一点都不会处于该函数曲面的下方,如下图所示。(把稳,这只是一种剖断方法,实际上还有许多其它的剖断方法,由于比较超纲以是不多先容了)
凸优化问题的例子包括支持向量机、线性回归等线性模型,非凸优化问题的例子包括低秩模型(如矩阵分解)、深度神经网络模型等,凸函数和优化算法没有直接的关系,对付模型而言其目标函数是凸函数,不一定利用梯度低落法进行求解,例如GMM的目标函数(带隐变量的极大似然函数)利用EM算法进行迭代求解。
自动化机器学习:问:模型和超参数有哪些自动化调优方法?它们各自有什么特点?
问:简述贝叶斯优化中用高斯过程回归打算目标函数后验分布的方法。高斯过程回归可以用于种类型或者层次型模型配置参数的优化吗?
问:贝叶斯优化中的得到函数是什么?起到什么浸染?请先容常用的得到函数。
模型运用和特色工程部分:问:什么是偏差和方差?偏差指的是由所有采样得到的大小为_m_的演习数据集演习出的所有模型的输出的均匀值和真实模型输出之间的差异。偏差常日是由于我们对学习算法做了缺点的假设所导致的,比如真实模型是某个二次函数,但我们假设模型是一次函数。由偏差带来的偏差常日在演习偏差上就能表示出来
方差指的是由所有采样得到的大小为_m_的演习数据集演习出的所有模型的输出的方差。方差常日是由于模型的繁芜度相对付演习样本数_m_过高导致的,比如一共有100个演习样本,而我们假设模型是阶数不大于200的多项式函数。由方差带来的偏差常日表示在测试偏差相对付演习偏差的增量上。
问:如何从减小方差和偏差的角度阐明Boosting和Bagging的事理?数据洗濯:非常值怎么判断?箱型图:上界怎么定义?极度非常值怎么判断?
怎么补充?用缺失落值补充,缺失落值怎么处理?
1.为什么利用中位数对缺失落值进行添补,这样做的好处是什么?
5.one-hot编码的事理及意义?
6.特色维度很高时你是若何做的操作?
标准化的适用场景、不适应场景?
所有模型都哀求对数据进行标准化么?
如果onehot等操作之后维度过高你会怎么做;
为什么K折交叉验证能防止过拟合?问:一样平常怎么做交叉验证.
缺失落值怎么处理?验证集怎么划分?哪些指标解释你的模型调优了?调节过模型的哪些参数
非常值的影响,如何肃清
连续特色分桶都有哪些方法(没说够) 卡方分箱那些的几个分箱策略的利用场景和优缺陷如何做数据预处理你理解哪些归一化办法(没说够)零均值归一化是线性的么为什么要离散化,离散化的参数如何确定
演习集和测试集分布不一致的问题是怎么创造的,怎么诊断定位,除了可视化还有没有其他直不雅观的指标
1.种别特色编码办法有哪些?如何办理 target encoding 的 target leakage?count encoding 有个缺陷:测试集和演习集分布不同,导致特色频率不一样。怎么办理?
为什么须要打算特色主要性,打算特色主要性的方法有哪些
连续特色怎么分箱,如何判断分箱的结果是好是坏
特色平滑方法有哪些
什么样的 ID 经由 Embedding 后可能有效,如何筛选有效的 ID。有些 ID 数量级很大,怎么处理
1. 哪些算法须要对特色前辈行归一化,这类算法有什么特点,不进行归一化的缺陷是?
5. #### 常见的筛选特色的方法有哪些?⭐⭐⭐⭐⭐
6. #### 数据怎么洗濯,缺失落值怎么添补⭐⭐⭐⭐⭐
7. #### 涌现Nan的缘故原由⭐⭐⭐⭐⭐
8. #### 特色筛选,怎么找出相似性高的特色并去掉⭐⭐⭐⭐⭐
11. #### 种别型数据你是如何处理的?比如游戏品类,地域,设备⭐⭐⭐⭐
12. #### 打算特色之间的干系性方法有哪些?⭐⭐⭐⭐
卡方考验的事理?
问:如何判断一个模型是处于高方差还是高偏差?高方差如何调节模型,高偏差如何调节模型?过拟合产生的缘故原由有哪些?如何防止过拟合?
特色选择的方法有哪些?过滤式,包裹式,嵌入式特色选择,过滤式特色选择紧张采取独立于模型的评估指标来评估特色的好坏,打算快,能够方便迅速的对特色进行粗筛,毛病在于 评估指标的打算与模型解耦,很多时候精度都不好,
问:那请你阐明一下什么是偏差和方差和泛化偏差,过拟合和欠拟合,怎么衡量一样平常?问题1 在模型评估过程中,过拟合和欠拟合详细是指什么征象?
一样平常我们阐明模型的泛化性能会用到偏差-方差分解,模型在演习阶段的预测和演习标签的偏离程度为偏差,刻画模型的拟合能力,模型在样本数相同的不同演习数据集下偏差的期望为方差,刻画数据变革对模型噪声的影响,泛化偏差=偏差+方差+噪声,噪声是模型所能达到的期望泛化偏差的下界,刻画了模型在学习当前问题本身的难度。
当然,这只是一种用于阐明模型泛化偏差的很理论的说法,我们在运用的过程中更常提到的是过拟合和欠拟合,过拟合意味着模型在演习集上的预测偏差和模型在验证集上的预测偏差存在较大差异,欠拟合则意味着模型在演习集上的预测偏差本身就比较大,在验证集上的预测偏差每每也会比较大。而所谓泛化偏差,我们也称之为泛化能力等,在实际运用的时候一样平常指的是模型对未知数据的预测能力,这个能力是根据预测的偏差决定的。
问:在模型评估过程中,过拟合和欠拟合详细是指什么征象?过拟合是指模型对付演习数据拟合呈过当的情形,反响到评估指标上,便是
模型在演习集上的表现很好,但在测试集和新数据上的表现较差。欠拟合指的是
模型在演习和预测时表现都不好的情形。
断交nfa办理方法:
数据,特色,模型
问:有没有碰着过模型在演习集上预测偏差大,在测试集上预测偏差小的情形?为什么会发生这种情形?答:有,模型恰好在验证数据上的泛化性能好,例如二分类问题中,测试集数据恰好是和分界超平面间隔很远的样本或者是回归问题中,验证数据在模型的拟合曲面上;
问:为什么会发生过拟合和欠拟合,怎么办理模型的过拟合和欠拟合的问题?这是一道很好回答又很难回答的口试题,之以是很好回答是由于有很多直不雅观的思路可以阐明过拟合和欠拟合,很难回答是由于很多的答案都无法回到过拟合和欠拟合的实质上导致了不同场景下不能自洽的问题;
在实际运用的过程中,实际上没有什么绝对的准则:
过拟合:
样本层面:大部分情形下增加样本可以缓解过拟合,少部分情形下减少样本可以缓解过拟合;
特色层面:大部分情形下减少特色可以缓解过拟合,少部分情形下增加特色可以缓解过拟合;
模型层面:约束模型的繁芜程度;不同模型有不同的约束办法,lr 有l1,l2或l1+l2,树模型有增大行列采样比例,限定树深,学习率放缩,早停等等,nn有dropout,bn等等,这是模型本身的处理,除此之外对模型进行集成也可在一定程度上缓解过拟合;
欠拟合:
同上,倒过来即可
问:为什么增加或减少样本会影响过拟合问题?为什么对特色的增减会影响过拟合问题?为什么约束模型的繁芜程度会缓解过拟合问题?首先,上述所提到的三种方法都是一种履历性的办理方法,并不一定见效,存在条件条件.
过拟合分为两种过拟合的情形:
1 在当前数据集上的过拟合;
2 在未来未知的数据集上的过拟合
在当前的数据集上的过拟合的评估涉及到train和valid数据集,一样平常我们剖断过拟合是否发生,便是打算model在train数据,即X_train和y_train上的metrics和在valid数据,即X_valid和y_valid上的metrics的差异从而衡量过拟合的程度;
在未来的数据集上的过拟合的评估则涉及到模型构建调度完毕之后,对未来的test数据集的评估,即X_test和y_test,当然y_test不一定是可得到的,很多时候通过实际的业务目标的达成情形来评估模型是否过拟合;
潜在的全量数据(这样的数据一样平常是不可获取的,这里面有两个缘故原由,
1.样本的获取是具有代价的,很难全面的采集所有干系的数据,纵然采集全面,如此巨量数据的存储和处理也是一个难以办理的问题;
2.样本是具有韶光属性的,我们无法采集到未来的数据,而我们要预测的恰好也是未来的数据)
这里我们假设潜在的全量数据为X,潜在的真实标签为y
须要明确三点:
存在假设:建模的条件之一是培植X和y存在某种映射关系,我们利用有限的train和test来演习模型逼近这个隐式的映射关系,利用train上拟合的模型预测test来有偏的考验模型的泛化能力;稳定假设:我们假设真实的 X-->y的映射关系是静态不变的,即所谓 独立同分布;乐不雅观假设:我们假设用于模型演习的数据train具有足够的代表性,能够代表未来的所有样本回到问题上,现在假设我们在train和test上的预测的metrics差异很大,即涌现了当前数据集上的过拟合问题,则我们须要这么剖析(把稳,下面是对当前过拟合问题的剖析):
1 当X-->y的映射关系不存在的时候,无论利用什么方法,我们都无法办理当前过拟合问题或未来过拟合问题,,模型的预测结果是无意义的,例如利用淘宝商品的价格预测华盛顿的温度,这种情形一样平常在利用train和valid数据进行模型构建和验证的阶段就会创造;
2.当X-->y 的映射关系存在且稳定,则
在当前的train和test的数据集上涌现过拟合的缘故原由在于train和test数据集不相似,或者说train数据集相对付test数据集是有偏的,这个时候增加数据有可能缓解模型的过拟合问题,例如我们引入的数据恰好和test相似乃至和test完备一样的样本,则此时在test上的metrics评估结果会大大改进,例如对图像做翻转可以作为cv中的一种基本的数据增强的办法紧张缘故原由在于test数据集中也会存在翻转的图像;
但是如果引入的数据完备和test不同,则对付模型在test上的评估是没有帮助乃至可能起到负效果,这种情形下引入的样本我们常常称之为噪声样本,例如通过上采样的办法对构造化数据进行样本天生很随意马虎产生这种噪声样本,;
这个时候增加或者减少特色也是可能缓解过拟合问题的,
问:为何模型总是难以拟合真实情形问:为什么你认为增加样本、减少特色,约束模型繁芜度,能够办理过拟合问题?答:由于我紧张打仗的是表格数据,以是,就表格数据来谈这个问题吧,在表格数据里增加样本的办法无非是通过一些代价得到更多的真实数据和标签,另一种办法便是通过一些上采样的办法来做数据增强,增加的是伪数据。
首先,过拟合的实质是数据分布的变革,而所谓的数据分布的实质是特色的分布,而我们所关注的“分布”是相对付模型而言的,例如对付gbdt来说,特色主要性最高的特色群的分布才是我们紧张关注的,特色主要性很低乃至为0的特色我们基本不怎么考虑他们的分布是否发生变革,因此,“分布”和"模型"是紧密干系的,纵然是无监督的背景下,我们也会根据业务履历重点关注一些认为比较主要的特色的分布进行follow,跳回来说,空想状态下如果数据的分布是完备同等的,则我们实在根本不用考虑模型的繁芜度或者降落特色维度的问题,比如说二分类问题吧,如果正负样本是完备线性可分的,并且未来的新样本的分布完备同等,则gbdt拟合1亿棵树都不会有过拟合的问题;
以是,之以是模型会发生过拟合,是由于未来的数据的部分特色的分布或者是部分特色的联合分布发生了变革从而导致模型的预测出错,有两种情形:
1、肉眼可见的特色的取值发生变革了,例如演习集的特色的取值范围在0~1之间,预测数据的特色的取值范围为0~10之间;
2、特色的取值可能没有明显变革,但是特色的联合分布发生变革了,一个大略例子,两列种别特色,f1和f2,f1的取值为a,b,f2的取值为A,演习集中f1和f2的组合为aA,aB,测试集中涌现了bA.
增加数据能够缓解过拟合的情形在于我们增加的数据引入了更多会未来将涌现的样本相似或完备相同的样本,但是如果引入的数据和未来的样本完备不相似,例如不屈衡学习中的许多上采样的方法,纯粹基于演习数据的一些加减打算,难以扩充和未来相似的样本,自然是不能缓解过拟合问题了;
回到问题,增加样本可能可以缓解过拟合问题但并不绝对,之以是有时候能够缓解过拟合问题
问:为什么须要对数值类型的特色做归一化?1.通过梯度低落法求解的模型常日是须要归一化的,包括线性回归、逻辑回归、基于梯度低落法视角下的支持向量机、神经网络等模型,紧张缘故原由在于归一化能够大大加快梯度低落法收敛的速率,
具有相似尺度的特色可以帮助梯度低落更好更快地收敛;
具有不同程度的幅度和范围的特色将导致每个特色的步长不同。因此,为了确保梯度低落更平滑、更快速地收敛,我们须要缩放我们的特色,使它们共享相似的尺度;
(逻辑回归的梯度公式比拟一下就造了)
2.基于间隔打算的模型例如范例的knn,kmeans等对付不同量纲下的特色的间隔打算非常敏感,这个缘故原由很大略不多阐明了;
问 在对数据进行预处理时,该当若何处理种别型特色?特色编码,onehot,woe,target encoding等(详细编码方法可以参考category encoding),lgb内部实在做的是梯度编码也算是一种编码的方法,深度学习里可以利用embedding等;
问:什么是组合特色?如何处理高维组合特色?为了提高繁芜关系的拟合能力,在特色工程中常常会把一阶离散特色两两组合,构成高阶组合特色
广义线性模型问:什么是广义线性模型?问:推导一下线性回归和l逻辑回归?逻辑回归:
y_pred=sigmoid(wx) ,x的增加一个维度为1,这样截距项直接包含到w里,形式上更简洁和影象。
丢失函数:二元交叉熵,
个中:
合并同类项,y_pred带入,就可以得到简化的二元交叉熵:
对W求导可得:
=
推导完毕。
线性回归:
追问:为什么做线性回归,逻辑回归之前要做归一化?
从上面的梯度打算公式可以看出来了,特色两个不一样,则W权重中的每一个wi的梯度更新量差异很大,量纲大的特色对应的权重w的梯度更新的量纲也大。导致梯度中的偏导差异极大,使得模型收敛很慢乃至无法收敛。
问:逻辑回归的丢失是若何的,逻辑回归丢失为什么这么设计问:逻辑回归丢失函数中为啥要加1/N
1/N(N表示样本数量)可以领悟到learning rate里去理解,torch的丢失函数里面也设计了 对loss进行均匀和对loss进行求和,均匀不求和的差异就在于每一个step对参数w的梯度更新量的差异为N(样本数量)倍,数据量很大时,会导致梯度更新量非常大,权重的变革会非常的剧烈,收敛困难,以是用1/N,不过实在learning rate缩小n倍达到的效果是一样的。
梯度表达式前面的以乘数的形式存在的常数项对梯度低落法的收敛没有任何的影响,实质上可以理解为learning rate的变革。
问:逻辑回归利用梯度低落法的时候的停滞条件是什么?1、达到最大迭代次数
2、所有的权重的梯度更新量的值都小于预先设定的阈值
3、早停等.
问:逻辑回归是线性模型还是非线性模型?这个地方很故意思,这涉及到我们怎么去定义线性还是非线性(1.根据模型的决策超平面来定义模型的线性和非线性,一样平常比较难,很难画出高维超平面;2.模型的参数是否是线性组合的,tree和nn的参数都是非线性组合的形式),如果从输出的角度来看,逻辑回归输出的是非线性的数据,经由sigmoid映射之后的输出值是非线性的:
但是如果我们从他的决策面来说,它又是超平面而不是曲面:
上述征象的缘故原由是:
sigmoid函数便是一个纯粹的数学变换没有任何的可学习参数,我们的决策是直接根据右边的式子得到的,sigmoid只是卖力映射成非线性的输出罢了,直不雅观的说便是我们的逻辑回归的输出在进入sigmoid函数之前是图2这样的线性的值,经由sigmoid之后称为非线性的值,以是从决策平面的来说逻辑回归是线性模型,从输出来看逻辑回归是非线性模型,不过一样平常是从决策平面来定义线性和非线性的,以是我们还是将逻辑回归视为线性模型。
严格的定义:模型的参数是否是线性组合的
问:试着从3个角度来阐明逻辑回归?(1、概率角度剖析逻辑回归;2、GLM角度剖析线性回归和逻辑回归;3、最大熵模型和逻辑回归的关联;)lr之以是能衍生出很多口试的问题,紧张在于逻辑回归这个模型可以从很多角度阐明,每个角度所代表的领域知识各不相同,是一个非常好的稽核口试者的机器学习根本的问题,以是这种题目基本上不会断。
问:为什么逻辑回归要用极大似然法来进行参数估计?极大似然估计是一种参数估计的方法,它是频率学派最经典的方法之一,认为真实发生的结果的概率该当是最大的,那么相应的参数,也该当是能让这个状态发生的概率最大的参数。大略说便是如果事宜发生了被我们不雅观测到了,那么这个事宜对应发生的概率一定是最大的才能被我们不雅观测到否则就不会被我们不雅观测到,以是当前的状态是这个事宜发生概率最大的结果。
逻辑回归假设数据服从伯努利分布,则P(y|X)——在已知x的情形下y服从伯努利分布,通过极大化似然函数的方法,利用梯度低落或者拟牛顿法等最优化方法来求解参数,以达到将数据二分类的目的。
逻辑回归与线性回归的差异(由于项目中有用到逻辑回归)、p值、假设考验、参数估计、方差和标准差的差异(自己平时如何利用他们)
LR为什么用sigmoid函数。这个函数有什么优点和缺陷?为什么不用其他函数?sigmoid函数由那个指数族分布,加上二项分布导出来的。丢失函数是由最大似然估计求出的。
naive bayes和logistic regression的差异为什么LR须要归一化或者取对数,为什么LR把特色离散化后效果更好,、逻辑回归为啥利用sigmoid函数,有何优缺陷逻辑回归中为啥用对数,并且为啥不用log而用ln(1) 为什么可以用 Sigmoid 函数定义了逻辑回归的条件概率,<w,x>的内积代表数据属于正类(y=1)的确信度。<w,x>越大则x属于正类的确信度越大。由于建模需求,须要将<w,x>从全体实数空间映射到条件概率P(y=1|w,x),Sigmoid 函数单调递增能反响确信度,并且能够将实数空间(-无穷,+无穷)映射到(0,1)区间内,能表示概率意义,更加直不雅观。
(2) 为什么要用:指数分布具有最大熵的性子,即在知足条件假设下的分布,分布越均匀越好.在逻辑回归中认为P(Y|x)服从伯努利二分布,并且P(y|x)=f(wx),可根据最大熵的性子推出sigmoid函数。
如果逻辑回归的所有样本的都是正样本, 那么它学出来的超平面是若何的?LR推导(伯努利过程,极大似然,丢失函数,梯度低落)有没有最优解?LR可以用核么?可以怎么用?l1和l2正则项是啥?lr加l1还是l2好?加哪个可以用核(加l2正则项,和svm类似,加l2正则项可以用核方便处理)LR可以用来处理非线性问题么?(还是lr啊 只不过是加了核的lr 这里加核是显式地把特色映射到高维 然后再做lr)怎么做?可以像SVM那样么?为什么?SVM和logistic回归分别在什么情形下利用?https://www.zhihu.com/question/21704547逻辑斯蒂回归能否办理非线性分类问题?https://www.zhihu.com/question/29385169逻辑回归估计参数时的目标函数逻辑回归的值表示概率吗?(值越大可能性越高,但不能说是概率)为什么把特色组合之后还能提升,反正这些基本都是增强了特色的表达能力,或者说更随意马虎线性可分吧逻辑回归对特色有什么哀求,是否须要做离散化,离散化的好处与坏处。L1 和 L2 正则化的差异L0 范数:向量中非0元素的个数。
L1 范数 (Lasso Regularization):向量中各个元素绝对值的和。
L2 范数(Ridge Regression):向量中各元素平方和再求平方根。
L0 范数和 L1 范数都能够达到使参数稀疏的目的,但 L0 范数更难优化求解,L1 范数是 L0 范数的最优凸近似,而且它比 L0 范数要随意马虎优化求解。
L2 范数不但可以防止过拟合,提高模型的泛化能力,还可以让我们的优化求解变得稳定和快速。L2 范数对大数和 outlier 更敏感!
· LR(5星):丢失函数、交叉熵、权重更新的推导(建议每次口试之前推一遍);从权重更新的公式中,明白交叉熵相对付MSE丢失函数的优点(大部分CNN网络构造用的丢失函数都是交叉熵);多个角度阐明逻辑回归与SVM之间的关系;标签是-1/1时丢失函数形式推导。
线性回归(4星):权重更新办法的推导,包括矩阵形式的和非矩阵形式的(西瓜书上有);包含L1或者L2正则化的权重更新的推导;L1/L2正则化包含的贝叶斯先验假设(或者从多个角度阐明L1/L2对特色选择的浸染);在包含重复特色情形下,线性回归存在的问题,L1正则化是否能办理等细节问题。
为什么交叉熵丢失函数有log项?
.lr的基本事理,为什么要用sigmoid的函数,最大熵模型是否理解过
LR模型里面有共线性的问题怎么办理?
逻辑回归采取的是交叉熵,那你 知道相对熵(KL)吗?
问:手写一下逻辑回归的丢失函数,推导逻辑回归为什么不用最小二乘? 基于mse来进行模型求解的称之为最小二乘法
l1 l2正则差异
LR的基本假设(当时没回答出来,该当是知足伯努利分布)
LR的缺陷
lr中特色干系性较高会若何(多重共线性)(10个干系性很高的特色)
什么时候lr比xgb好
对付LR来说,LR如果多了一维冗余特色,其权重和AUC会若何变革(权重变为1/2, AUC不会变革)
什么情形下须要将连续变量分桶
为什么LR模型又可称最大熵模型?
逻辑回归怎么分类非线性数据?
逻辑回归引入查究法后丢失函数如何求导?
LR可以处理非线性问题吗
L1 L2的浸染,为什么有这样的浸染?一样平常求L1的优化方法(坐标低落,LARS角回归)
L1为什么能让参数稀疏,L2为什么会让参数趋于较小值,L1优化方法
LR模型中为何利用交叉熵而不该用MSE作为丢失函数(从丢失函数建立的目标和效果上谈)
Logistic Regression的事理及其推导;
8、 L2正则的实质?限定解空间范围,缩小解空间,掌握模型繁芜度
svm怎么用于多分类
svm的推导,什么是凸函数,为什么拉格朗日对偶方程成立
svm与lr的比拟与差异
svm系列,参考一下书问题1 在空间上线性可分的两类点,分别向SVM分类的超平面上做投影,这些点在
超平面上的投影仍旧是线性可分的吗?
Q:线性模型和决策树模型对特色选择特色利用有哪些差异
Q:决策树和线性模型哪个更好在线更新
写线性回归的解析解,矩阵不可逆怎么办?
4)SVM的对偶问题(我没想起来)
什么样的函数是核函数
如何去选择核函数,线性,高斯核函数。
讲了下SVM的推导:hard margin, soft margin, 几何间隔、函数间隔,最优化,拉格朗日乘子法,对偶问题,KKT条件,丢失函数,惩罚系数等。
为什么SVM求解哀求解他的对偶问题?
为了使原问题更好求解,由于原问题不好求解,引入对偶问题之后就更好求解了。
实在,是由于对偶问题可以降落原问题的打算繁芜度。
问题2 是否存在一组参数使SVM演习偏差为0?
问题3 演习偏差为0的SVM分类器一定存在吗?
问题4 加入松弛变量的SVM的演习偏差可以为0吗?
1. 问SVM算法事理,如果数据分布是同心圆怎么办?答核函数,然后便是讲述过程;
SVM的支持向量是什么?
梯度低落法是一阶导,牛顿法是二阶导?为什么还会有牛顿法的涌现?解释数学事理
SVM可以处理非线性问题吗
问了svm的推导,问的非常细,问间隔到底如何定义的,不可分的svm中松弛变量怎么理解,如果有个点特殊非常,是否还能找到分割面
svm的事理,smo算法,
svm的核函数的浸染,lr能不能用核函数,为什么
SVM的事理及其推导
手推svm
svm推导,核函数的表示,常用的核函数有哪些
为什么svm可以利用和函数,LR不可以利用
SVM事理,支撑向量越多越好还是越少越好
svm推导,为什么要用拉格朗日乘数法,对偶问题是什么
KKT条件都有什么,如何求解svm的最优化问题
2、特色工程做的有哪些?非线性可分的情形怎么处理的?
9、 SVM引入核函数实质?提高维度,增加模型繁芜度
Q:这样啊,那我手推一下SVM吧
Q:为什么必须知足KKT条件?
· SVM(5星):理解SVM目标函数的由来;理解SVM中核技巧的利用;将目标函数转化成对偶问题的推导(软间隔、硬间隔);为什么要转换成对偶问题求解,求解的权重个数(一系列干系的细节问题);多个角度阐明逻辑回归与SVM之间的关系。
连续问有了P,R为什么要有AUC和F1-score(说AUC是真阳性,与假阳性之间的平衡,面积越大越好,然后F1-score,是平衡p和R)
说说SVM丢失函数
10. #### 最小二乘法在什么条件下与极大似然估计等价?⭐⭐⭐⭐⭐
如果特色比较多,用LR还是SVM?
SVM是否可以用随机梯度低落
为什么要将求解 SVM 的原始问题转换为其对偶问题
为什么SVM对缺失落数据敏感
SVM怎么防止过拟合 ?
【机器学习】
【机器学习】SVM的高斯核函数公式是什么?为什么办理非线性问题一定要用核函数?各种核函数的公式
贝叶斯和统计:1.有一个场景,想用朴素贝叶斯,但效果不好,怎么优化?
2.朴素贝叶斯公式是怎么得到的,推导一下
3.常见分布 + 常见假设考验 + p-value打算
4.偏度和峰度
5.先验概率、条件概率
6.写一下贝叶斯公式
7.贝叶斯公式,实际如何打算,如何办理精度问题。
8.朴素贝叶斯的证明(不懂)
9.朴素贝叶斯适用哪些场景
人以为很少有口试官会直接问贝叶斯决策,最多就问一个先验概率和后验概率的联系,但是朴素贝叶斯的思想会在很多算法中表示,比如L1、L2正则化的贝叶斯先验假设,期望最大化算法与最小二乘法的联系,k-means包含的贝叶斯先验假设等。以是理解贝叶斯的思想是核心。
马尔科夫模型(1星,提问概率极低):3个基本问题以及对应求解算法,要理解(前向后向算法、B-W算法、维特比算法)
贝叶斯定理,全概率公式1.朴素贝叶斯优缺陷⭐⭐⭐⭐⭐
2.贝叶斯公式⭐⭐⭐⭐⭐
3.朴素贝叶斯中的“朴素”怎么理解?⭐⭐⭐⭐⭐
4.什么是拉普拉斯平滑法?⭐⭐⭐⭐⭐
5.朴素贝叶斯中有没有超参数可以调?⭐⭐⭐⭐⭐
6.你知道朴素贝叶斯有哪些运用吗?⭐⭐⭐⭐⭐
7.朴素贝叶斯对非常值敏不敏感?⭐⭐⭐⭐⭐
8.频率学派与贝叶斯学派的差别⭐⭐⭐
9.概率与期望的公式⭐⭐⭐⭐
10.先验概率与后验概率⭐⭐⭐⭐
矩阵分解 和降维:1.先容PCA,特色值分解,奇异值分解等等(描述了这两个分解的意义,特色值和特色向量的用场以及这两个分解的运用)
2.PCA事理及涉及的公式
3.PLSA和LDA的联系差异
4.降维有哪些方法+
5.降维方法,PCA事理
6.降维的办法(PCA、LDA):算法思想,PCA特色降维公式推导。
7.PCA降维后对模型的准确率有何影响?
8.非负矩阵分解的丢失函数是什么?
其它:1.有监督学习和无监督学习的差异是什么.
2.半监督学习里无标签样本的打标
3.天生模型和判别模型的差异并且举例
4.如果分类样本的标签只有一定的概率可信,如何处理
5.KNN先容一下,优缺陷?KNN的K值怎么选?KNN数据须要归一化吗? KNN三要素说一下。 knn的k设置的过大会有什么问题?
6.样本服从t分布,怎么补充非常值
















