1、韶光繁芜度
韶光繁芜度便是是一个函数,这个函数含有两个变量,一个算法的运行韶光,一个算法要处理数据的数量。这里有一个关系:处理数据的数量越大,算法运行的次数和韶光越长。假设处理数据的数量是n,算法运行的次数便是f(n)。这里的f()是一个函数,它的大小随着n增大而增大,数学上叫单调递增函数。

以是,在打算韶光繁芜度T(n)的时候,步骤如下: 1、先要拿出算法的基本单元。 2、根据相应的各语句确定它的实行次数f(n)。 3、找出T(n)的同数量级,将这个同数量等级赋值给f(n)。 4、由于T(n)/f(n)求极限可以得到一个常数C。(求极限值是高档数学内容,自行百度脑补一下),我们可以确定韶光的繁芜度T(n) = O(f(n));
总结:常用的韶光繁芜度所耗费的韶光从小到大依次是:O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)。随着问题规模n的不断增大,上述韶光繁芜度不断增大,算法的实行效率越低。
2、空间繁芜度
空间繁芜度是指算法在内存内所须要的存储空间的度量,一样平常是指除正常占用内存开销外的赞助存储单元规模。和韶光繁芜度类似,这样标记:S(n)=O(f(n))。n为问题规模,f(n)为语句关于n所占存储空间的函数;
3、PHP冒泡排序法
PHP
$arr = array();for($i=0;$i<10000;$i++){ $arr[] = mt_rand(1,100000); } $t1 = microtime(true); //这是一个中间变量 $temp=0; //我们要把数组,从小到大排序 //外层循环 $flag=false;//这个优化之后效率会很高,一样平常够用 for($i=0;$i<count($arr)-1;$i++){ for($j=0;$j<count($arr)-1-$i;$j++){ //解释前面的数比后面的数大,就要交流 if($arr[$j]>$arr[$j+1]){ $temp=$arr[$j]; $arr[$j]=$arr[$j+1]; $arr[$j+1]=$temp; $flag=true; } } if(!$flag){ //已经是有序了 break; } $flag=false; } $t2 = microtime(true); echo $t2 -$t1;
算法部分代码均匀运行韶光(php 5.6): 11.246428012848 冒泡算法的均匀韶光繁芜度为:O(n2)
4、PHP选择排序法
选择排序法思路: 每次选择一个相应的元素,然后将其放到指定的位置
PHP
//实现思路 双重循环完成,外层掌握轮数,当前的最小值。内层 掌握的比较次数 $arr=array(); for($i=0;$i<10000;$i++){ $arr[] = mt_rand(1,100000); } $t1 = microtime(true); //这是一个中间变量 $temp=0; for($i=0;$i<count($arr)-1;$i++){ //假设$i便是最小的数 是须要参与比较的元素 $minVal=$arr[$i]; //记录我认为的最小数的下标 $minIndex=$i; for($j=$i+1;$j<count($arr);$j++){ //解释我们认为的最小值,不是最小 if($minVal>$arr[$j]){ $minVal=$arr[$j]; $minIndex=$j; } } //末了交流 $temp=$arr[$i]; $arr[$i]=$arr[$minIndex]; $arr[$minIndex]=$temp; } $t2 = microtime(true); echo $t2 -$t1;
算法部分代码均匀运行韶光 6.1832849979401 快速排序法均匀韶光繁芜度:O(n2)
5、插入排序法(小到大排序)
效率又比 选择排序法要高一些 插入排序法思路:将要排序的元素插入到已经 假定排序号的数组的指定位置
PHP
$arr=array(); for($i=0;$i<10000;$i++){ $arr[] = mt_rand(1,100000); } $t1 = microtime(true); //先默认下标为0的这个数已经是有序 for($i=1;$i<count($arr);$i++){ //$insertVal是准备插入的数 $insertVal=$arr[$i]; //准备先和谁下标为$inserIndex的比较 $inserIndex=$i-1; //如果这个条件知足,解释我们还没有找到适当的位置 while($inserIndex >= 0 && $insertVal < $arr[$inserIndex]){ //同时把数后移 $arr[$inserIndex+1] = $arr[$inserIndex]; $inserIndex--; } //插入(这时就给$inserIndex找到适当的位置) $arr[$inserIndex+1] = $insertVal; } $t2 = microtime(true); echo $t2 -$t1;
算法部分代码均匀运行韶光 2.6323339939117 插入法的均匀韶光繁芜度:O(n2)
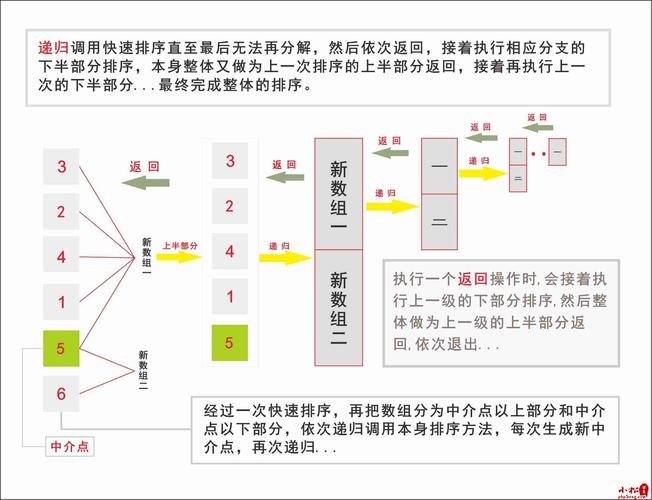
6、快速排序法
PHP
$arr=array(); for($i=0;$i<10000;$i++){ $arr[] = mt_rand(1,100000); } $t1 = microtime(true); $a = quick_sort($arr);$t2 = microtime(true); echo $t2 -$t1;function quick_sort($arr) { //先判断是否须要连续进行 $length = count($arr); if($length <= 1) { return $arr; } //如果没有返回,解释数组内的元素个数 多余1个,须要排序 //选择一个标尺 //选择第一个元素 $base_num = $arr[0]; //遍历 除了标尺外的所有元素,按照大小关系放入两个数组内 //初始化两个数组 $left_array = array();//小于标尺的 $right_array = array();//大于标尺的 for($i=1; $i<$length; $i++) { if($base_num > $arr[$i]) { //放入左边数组 $left_array[] = $arr[$i]; } else { //放入右边 $right_array[] = $arr[$i]; } } //再分别对 左边 和 右边的数组进行相同的排序处理办法 //递归调用这个函数,并记录结果 $left_array = quick_sort($left_array); $right_array = quick_sort($right_array); //合并左边 标尺 右边 return array_merge($left_array, array($base_num), $right_array); }
算法部分代码均匀运行韶光 0.055506944656372 快速排序法的均匀韶光繁芜度:O(nlog2n)
















