小叽导读:闲鱼是一款闲置物品的交易平台APP。通过这个平台,全国各地“无处安顿”的物品能够轻松实现流动。这种分享经济业务形态被越来越多的人所接管,也进一步实现了低碳生活的目标。
本日,闲鱼团队就商品与商圈的匹配算法为我们展开详细解读。

择要
闲鱼app根据交通条件、阛阓分布情形、住宅区分布情形综合考虑,将城市划分为一个个商圈。杭州部分区域商圈划分如下图所示。
闲鱼的商品是由用户发布的GPS随机分布在舆图上的点数据。当用户处于某个商圈范围内时,app会向用户推举GPS位于此商圈中的商品。要实现精准推举行事,就须要打算出哪些商品是归属于你所处的商圈。
在数据库中,商圈是由多个点围成的面数据,这些面数据形状、大小互异,且互不重叠。商品因此GPS标记的点数据,如何能够快速高效地确定海量商品与商圈的归属关系呢?传统而直接的方法是,利用几何学的空间关系打算公式对海量数据履行直接的“点—面”关系打算,来确定每一个商品是否位于每一个商圈内部。
闲鱼目前有10亿商品数据,且每天还在快速增加。全国所有城市的商圈数量总和大约为1万,每个商圈的大小不一,边数从10到80不等。如果直策应用几何学点面关系运算,须要的打算量级约为2亿亿次基本运算。按照这个思路,我们考试测验过利用阿里巴巴集团内部的离线打算集群来实行打算,结果集群在运行了超过2天之后也未能给出结果。
经由算法改进,我们采取了一种基于GeoHash精确匹配,结合GeoHash非精确匹配并合营小范围几何学关系运算精匹配的算法,大大降落了打算量,高效地实现了离线环境下海量点-面数据的包含关系打算。同样是对10亿条商品和1万条商圈数据做匹配,可以在1天内得到结果。
▌点数据GeoHash事理与算法
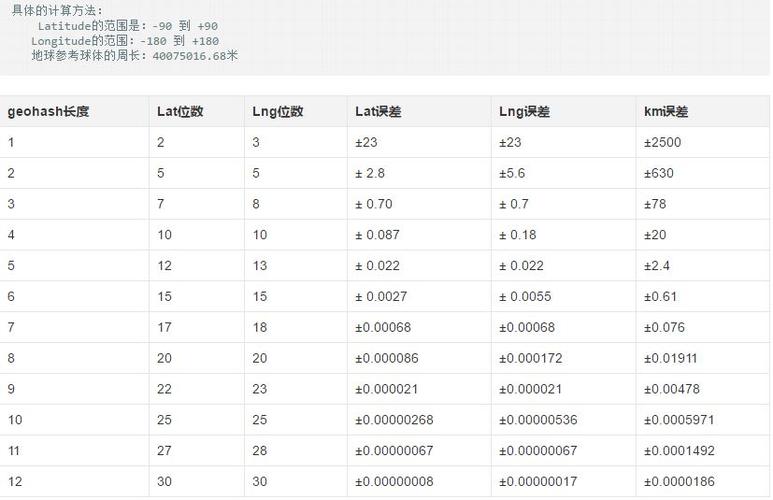
GeoHash是一种对地理坐标进行编码的方法,它将二维坐标映射为一个字符串。每个字符串代表一个特定的矩形,在该矩形范围内的所有坐标都共用这个字符串。字符串越长精度越高,对应的矩形范围越小。
对一个地理坐标编码时,按照初始区间范围纬度[-90,90]和经度[-180,180],打算目标经度和纬度分别落在左区间还是右区间。落在左区间则取0,右区间则取1。然后,对上一步得到的区间连续按照此方法对半查找,得到下一位二进制编码。当编码长度达到业务的进度需求后,根据“偶数位放经度,奇数位放纬度”的规则,将得到的二进制编码穿插组合,得到一个新的二进制串。末了,根据base32的对照表,将二进制串翻译成字符串,即得到地理坐标对应的目标GeoHash字符串。
以坐标“30.280245, 120.027162”为例,打算其GeoHash字符串。首先对纬度做二进制编码:
将[-90,90]平分为2部分,“30.280245”落在右区间(0,90],则第一位取1。
将(0,90]平分为2分,“30.280245”落在左区间(0,45],则第二位取0。
不断重复以上步骤,得到的目标区间会越来越小,区间的两个端点也越来越逼近“30.280245”。
下图的流程详细地描述了前几次迭代的过程:
按照上面的流程,连续往下迭代,直到编码位数达到我们业务对精度的需求为止。完全的15位二进制编码迭代表格如下:
得到的纬度二进制编码为10101 01100 01000。
按照同样的流程,对经度做二进制编码,详细迭代详情如下:
得到的经度二进制编码为11010 10101 01101。
按照“偶数位放经度,奇数位放纬度”的规则,将经纬度的二进制编码穿插,得到完成的二进制编码为:11100 11001 10011 10010 00111 00010。由于后续要利用的是base32编码,每5个二进制数对应一个32进制数,以是这里将每5个二进制位转换成十进制位,得到28,25,19,18,7,2。 对照base32编码表,得到对应的编码为:wtmk72。
可以在geohash.org/网站对上述结果进行验证,验证结果如下:
验证结果的前几位与我们的打算结果同等。如果我们利用二分法获取二进制编码时迭代更多次,就会得到验证网站中这样的位数更多的更精确结果。
GeoHash字符串的长度与精度的对应关系如下:
▌面数据GeoHash编码实现
上一节先容的标准GeoHash算法只能用来打算二维点坐标对应的GeoHash编码,我们的场景中还须要打算面数据(即GIS中的POLYGON多边形工具)对应的GeoHash编码,须要扩展算法来实现。
算法思路是,先找到目标Polygon的最小外接矩形MBR,打算此MBR西南角坐标对应的GeoHash编码。然后用GeoHash编码的逆算法,反解出此编码对应的矩形GeoHash块。以此GeoHash块为出发点,循环往东、往北找相邻的同等大小的GeoHash块,直到找到的GeoHash块完备超出MBR的范围才停滞。如此找到的多个GeoHash块,边缘上的部分可能与目标Polygon完备不相交,这部分块须要通过打算剔除掉,如此一来可以减少后续不必要的打算量。
上面的例子中终极得到的结果高清大图如下,个中蓝色的GeoHash块是与原始Polygon部分相交的,橘黄色的GeoHash块是完备被包含在原始Polygon内部的。
上述算法总结成流程图如下:
▌求附近GeoHash块的快速算法
上一节对面数据进行GeoHash编码的流程图中标记为绿色和橘黄色的两步,分别是要探求相邻的东边或北边的GeoHash字符串。
传统的做法是,根据当前GeoHash块的反解信息,求出相邻块内部的一点,在对这个点做GeoHash编码,即为相邻块的GeoHash编码。如下图,我们要打算\公众wtmk72\"大众周围的8个相邻块的编码,就要先利用GeoHash逆算法将\"大众wtmk72\"大众反解出4个顶点的坐标N1、N2、N3、N4,然后由这4个坐标打算出右侧毗邻块内部的任意一点坐标N5,再对N5做GeoHash编码,得到的“wtmk78”便是我们哀求的右边毗邻块的编码。按照同样的方法,求可以求出\公众wtmk72\公众周围统共8个毗邻块的编码。
这种方法须要先解码一次再编码一次,比较耗时,尤其是在指定的GeoHash字符串长度较长须要循环较多次的情形下。
通过不雅观察GeoHash编码表的规律,结合GeoHash编码利用的Z阶曲线的特性,验证了一种通过查表来快速求相邻GeoHash字符串的方法。
还是以“wtmk72”这个GeoHash字符串为例,对应的10进制数是“28,25,19,18,7,2”,转换成二进制便是11100 11001 10011 10010 00111 00010。个中,w对应11100,这5个二进制位分别代表“经 纬 经 纬 经”;t对应11001,这5个二进制位分别代表“纬 经 纬 经 纬”。由此推广开来可知,GeoHash中的奇数位字符(本例中的'w'、'm'、'7')代表的二进制位分别对应“经 纬 经 纬 经”,偶数位字符(本例中的't'、'k'、'2')代表的二进制位分别对应“纬 经 纬 经 纬”。
'w'的二进制11100,转换成方位含义便是“右 上 右 下 左”。't'的二进制11001,转换成方位含义便是“上 右 下 左 上”。
根据这个字符与方位的转换关系,我们可以知道,奇数位上的字符与位置对照表如下:
偶数位上的字符与位置对照表如下:
这里可以看到一个很故意思的征象,奇数位的对照表和偶数位对照表存在一种转置和翻转的关系。
有了以上两份字符与位置对照表,就可以快速得出每个字符周围的8个字符分别是什么。而要打算一个给定GeoHash字符串周围8个GeoHash值,如果字符串末了一位字符在该方向上未超出边界,则前面几位保持不变,末了一位取此方向上的相邻字符即可;如果末了一位在此方向上超出了对照表边界,则先求倒数第二个字符在此方向上的相邻字符,再求末了一个字符在此方向上相邻字符(对照表环状相邻字符);如果倒数第二位在此方向上的相邻字符也超出了对照表边界,则先求倒数第三位在此方向上的相邻字符。以此类推。
以上面的“wtmk72”举例,哀求这个GeoHash字符串的8个相邻字符串,实际便是求尾部字符‘2’的相邻字符。‘2’适用偶数对照表,它的8个相邻字符分别是‘1’、‘3’、‘9’、‘0’、‘8’、‘p’、‘r’、‘x’,个中‘p’、‘r’、‘x’已经超出了对照表的下边界,是将偶数位对照表高下相接组成环状得到的相邻关系。以是,对付这3个超出边界的“下方”相邻字符,须要求倒数第二位的下方相邻字符,即‘7’的下方相邻字符。‘7’是奇数位,适用奇数位对照表,‘7’在对照表中的“下方”相邻字符是‘5’,以是“wtmk72”的8个相邻GeoHash字符串分别是“wtmk71”、“wtmk73”、“wtmk79”、“wtmk70”、“wtmk78”、“wtmk5p”、“wtmk5r”、“wtmk5x”。利用此相邻字符串快速算法,可以大大提高上一节流程图中面数据GeoHash编码算法的效率。
▌高效建立海量点数据与面数据的关系
建立海量点数据与面数据的关系的思路是,先将须要匹配的商品GPS数据(点数据)、商圈AOI数据(面数据)按照前面所述的算法,分别打算同等长度的GeoHash编码。每个点数据都对应唯一一个GeoHash字符串;每个面数据都对应一个或多个GeoHash编码,这些编码要么是“完备包含字符串”,要么是“部分包含字符串”。
a)将每个商品的GeoHash字符串与商圈的“完备包含字符串”进行join操作。join得到的结果中涌现的<商品,商圈>数据便是能够确定的“某个商品属于某个商圈”的关系。
b)对付剩下的还未被确定关系的商品,将这些商品的GeoHash字符串与商圈的“部分包含字符串”进行join操作。join得到的结果中涌现的<商品,商圈>数据是有可能存在的“商品属于某个商圈”的关系,接下来对这批数据中的商品gps和商圈AOI数据进行几何学关系运算,进而从中筛选出确定的“商品属于某个商圈”的关系。
如图,商品1的点数据GeoHash编码为\公众wtmk70j\公众,与面数据的“完备包含字符串wtmk70j”join成功,以是可以直接确定商品1属于此面数据。
商品2的点数据GeoHash编码为“wtmk70r”,与面数据的“部分包含字符串wtmk70r”join成功,以是商品2疑似属于面数据,详细是否存在包含关系,还须要后续的点面几何学打算来确定。 商品3的点数据GeoHash编码与面数据的任何GeoHash块编码都匹配不上,以是可以快速确定商品3不属于此面数据。
实际运用中,原始的海量商品GPS范围散布在全国各地,海量商圈数据也散布在全国各个不同的城市。经由a)步骤的操作后,大部分的商品数据已经确定了与商圈的从属关系。剩下的未能匹配上的商品数据,经由b)步骤的GeoHash匹配后,可以将后续“商品-商圈几何学打算”的运算量从“1个商品 x 全国所有商圈”笛卡尔积的量级,降落为“1个商品 x 1个(或几个)商圈”笛卡尔积的量级,减少了绝大部分不必要的几何学运算,而这部分运算是非常耗时的。
在闲鱼的实际运用中,10亿商品和1万商圈数据,利用本文的快速算法,只须要 10亿次GeoHash点编码 + 1万次GeoHash面编码 + 500万次“点是否在面内部”几何学运算,粗略换算为基本运算须要的次数约为1800亿次,运算量远小于传统方法的2亿亿次基本运算。利用阿里巴巴的离线打算平台,本文的算法在不到一天的韶光内就完成了全部打算事情。
其余,对付给定的点和多边形,通过几何学打算包含关系的算法不止一种,最常用的算法是射线法。大略来说,便是从这个点出发做一条射线,判断该射线与多边形的交点个数是奇数还是偶数。如果是奇数,解释点在多边形内;否则,点在多边形外。
▌延伸
面对海量点面数据的空间关系划分,本文采取是的通过GeoHash来降落打算量的思路,实质上来说是利用了空间索引的思想。事实上,在GIS领域有多种实用的空间索引,常见的如R树系列(R树、R+树、R树)、四叉树、K-D树、网格索引等,这些索引算法各有特点。本文的思路不仅能用来处理点—面关系的干系问题,还可以用来快速处理点—点关系、面—面关系、点—线关系、线—线关系等问题,比如快速确定大范围类的海量公交站台与道路的从属关系、多条道路或铁路是否存在交点等问题。
本文作者:峰明
















