php牛顿迭代技巧_牛顿迭代法的可视化详解

以 Isaac Newton 和 Joseph Raphson 命名的 Newton-Raphson 方法在设计上是一种求根算法，这意味着它的目标是找到函数 f(x)=0 的值 x。
在几何上可以将其视为 x 的值，这时函数与 x 轴相交。

Newton-Raphson 算法也可以用于一些大略的事情，例如在给定之前的连续评估成绩的情形下，找出预测须要在期末考试中得到 A 的分数。
实在如果你曾经在 Microsoft Excel 中利用过求解器函数，那么就利用过像 Newton-Raphson 这样的求根算法。
其余一个繁芜用例是利用 Black-Scholes 公式反向求解金融期权合约的隐含颠簸率。

虽然公式本身非常大略，但如果想知道它实际上在做什么就须要仔细查看。

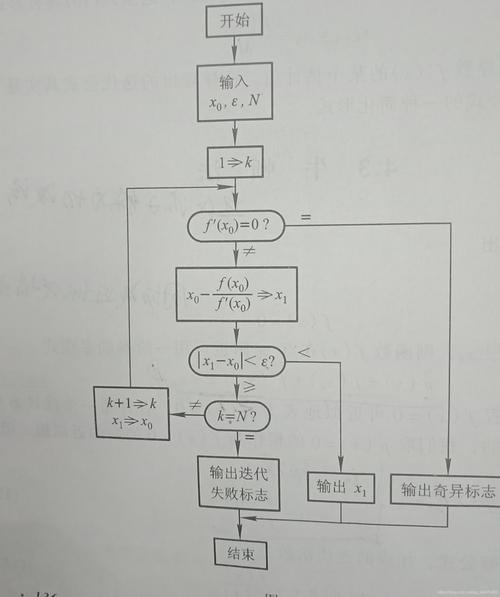
首先，让我们回顾一下整体方法：

1、初步预测根可能在哪里

2、运用 Newton-Raphson 公式得到更新后的预测，该预测将比初始预测更靠近根

3、重复步骤 2，直到新的预测足够靠近真实值。

这样就足够了吗？Newton-Raphson 方法给出了根的近似值，只管常日它对付任何合理的运用都足够靠近！
但是我们如何定义足够靠近？ 什么时候停滞迭代？

一样平常情形下Newton-Raphson 方法有两种处理何时停滞的方法。
1、如果预测从一个步骤到下一步的变革不超过阈值，例如 0.00001，那么算法将停滞并确认最新的预测足够靠近。
2、如果我们达到一定数量的预测但仍未达到阈值，那么我们就放弃连续预测。

从公式中我们可以看到，每一个新的预测都是我们之前的预测被某个神秘的数量调度了。
如果我们通过一个例子来可视化这个过程，它很快就会清楚发生了什么!

作为一个例子，让我们考虑上面的函数，并做一个 x=10 的初始预测（把稳这里实际的根在 x=4）。
Newton-Raphson 算法的前几个预测不才面的 GIF 中可视化

我们最初的预测是 x=10。
为了打算我们的下一个预测，我们须要评估函数本身及其在 x=10 处的导数。
在 10 处求值的函数的导数只是大略地给出了该点切线曲线的斜率。
该切线在 GIF 中绘制为 Tangent 0。

看下一个预测相对付前一个切线涌现的位置，你把稳到什么了吗？ 下一个预测涌如今前一个切线与 x 轴相交的位置。
这便是 Newton-Raphson 方法的亮点！

事实上， f(x)/f'(x) 只是给出了我们当前预测与切线穿过 x 轴的点之间的间隔（在 x 方向上）。
正是这个间隔见告我们每次更新的预测是多少，正如我们在 GIF 中看到的那样，随着我们靠近根本身，更新变得越来越小。

如果函数无法手动微分怎么办？

上面的例子中是一个很随意马虎用手微分的函数，这意味着我们可以毫无困难地皮算 f'(x)。
然而，实际情形可能并非如此，并且有一些有用的技巧可以在不须要知道其解析解的情形下逼近导数。

这些导数逼近方法超出了本文的范围，可以查找有关有限差分方法的更多信息。

敏锐的读者可能已经从上面的示例中创造了一个问题，纵然我们的示例函数有两个根（x=-2 和 x=4），Newton-Raphson 方法也只能识别一个根。
牛顿迭代会根据初值的选择向某个值收敛，以是只能求出一个值来。
如果须要别的值，是要把当前求的根带入后将方程降次，然后求第二个根。
这当然是一个问题，并不是这种方法的唯一缺陷：

梯度低落法和牛顿法都是迭代求解，不过梯度低落法是梯度求解，而牛顿法/拟牛顿法是用二阶的Hessian矩阵的逆矩阵或伪逆矩阵求解。
从实质上去看，牛顿法是二阶收敛，梯度低落是一阶收敛，以是牛顿法就更快。
如果更普通地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度低落法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。
可以说牛顿法比梯度低落法看得更远一点，能更快地走到最底部。
（牛顿高眼光更加长远，以是少走弯路；相对而言，梯度低落法只考虑了局部的最优，没有全局思想）。

那为什么不用牛顿法替代梯度低落呢？

实际上目前深度神经网络算法的收敛性本身便是没有很好的理论担保的，用深度神经网络只是由于它在实际运用上有较好的效果，但在深度神经网络上用梯度低落法是不是能收敛，收敛到的是不是全局最优点目前还都是无法确认的。
并且二阶方法可以得到更高精度的解，但是对付神经网络这种参数精度哀求不高的情形下反而成了问题，深层模型下如果参数精度太高，模型的泛化性就会降落，反而会提高模型过拟合的风险。

作者：Rian Dolphin