而所谓 单调栈 则是在栈的 前辈后出 根本之上额外添加一个特性:从栈顶到栈底的元素是严格递增(or递减)。
详细进展过程如下:

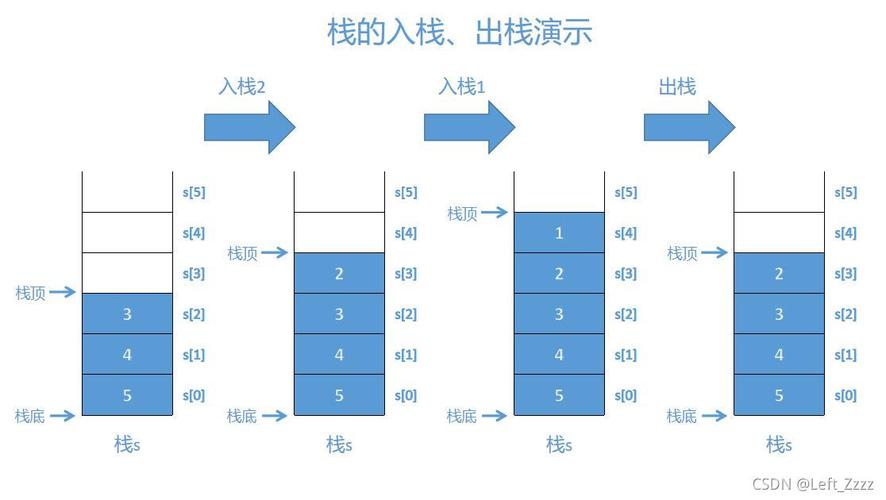
单调栈是一种分外的栈。栈本来便是一种受限的数据构造了,单调栈在此根本上又受限了一次
单调栈哀求栈中的元素是单调递减或者单调递减的。
是否严格递减或递减可以根据实际情形来。
这里我用 [a,b,c] 表示一个栈。 个中 左侧为栈底,右侧为栈顶。单调增还是单调减取决于出栈顺序。如果出栈的元素是单调增的,那便是单调递增栈,如果出栈的元素是单调减的,那便是单调递减栈。
比如:
[1,2,3,4] 便是一个单调递减栈(由于此时的出栈顺序是 4,3,2,1。下同,不再赘述)[3,2,1] 便是一个单调递增栈[1,3,2] 就不是一个合法的单调栈那这个限定有什么用呢?这个限定(特性)能够办理什么用的问题呢?
以 单调递增栈 为例进行解释。现在有一组数
3,4,2,6,4,5,2,3
让它们从左到右依次入栈。
详细过程如下:
单调栈的用场
单调栈适宜的题目是求解下一个大于 xxx或者下一个小于 xxx这种题目。以是当你有这种需求的时候,就该当想到单调栈。
那么为什么单调栈适宜求解下一个大于 xxx或者下一个小于 xxx这种题目?缘故原由很大略,我这里通过一个例子给大家讲解一下。
这里举的例子是单调递减栈
比如我们须要依次将数组 [1,3,4,5,2,9,6] 压入单调栈。
首先压入 1,此时的栈为:[1]连续压入 3,此时的栈为:[1,3]连续压入 4,此时的栈为:[1,3,4]连续压入 5,此时的栈为:[1,3,4,5]如果连续压入 2,此时的栈为:[1,3,4,5,2] 不知足单调递减栈的特性, 因此须要调度。如何调度?由于栈只有 pop 操作,因此我们只好不断 pop,直到知足单调递减为止。上面实在我们并没有压入 2,而是先 pop,pop 到压入 2 依然可以保持单调递减再 压入 2,此时的栈为:[1,2]连续压入 9,此时的栈为:[1,2,9]如果连续压入 6,则不知足单调递减栈的特性, 我们故技重施,不断 pop,直到知足单调递减为止。此时的栈为:[1,2,6]把稳这里的栈仍旧是非空的,如果有的题目须要用到所有数组的信息,那么很有可能因没有考虑边界而不能通过所有的测试用例。 这里先容一个技巧 - 哨兵法,这个技巧常常用在单调栈的算法中。
对付上面的例子,我可以在原数组 [1,3,4,5,2,9,6] 的右侧添加一个小于数组中最小值的项即可,比如 -1。此时的数组是 [1,3,4,5,2,9,6,-1]。这种技巧可以简化代码逻辑,大家只管即便节制。
上面的例子如果你明白了,就不难明得为啥单调栈适宜求解下一个大于 xxx或者下一个小于 xxx这种题目了。比如上面的例子,我们就可以很随意马虎地求出在其之后第一个小于其本身的位置。比如 3 的索引是 1,小于 3 的第一个索引是 4,2 的索引 4,小于 2 的第一个索引是 0,但是其在 2 的索引 4 之后,因此不符合条件,也便是不存在在 2 之后第一个小于 2 本身的位置。
上面的例子,我们在第 6 步开始 pop,第一个被 pop 出来的是 5,因此 5 之后的第一个小于 5 的索引便是 4。同理被 pop 出来的 3,4,5 也都是 4。
如果用 ans 来表示在其之后第一个小于其本身的位置,ans[i] 表示 arr[i] 之后第一个小于 arr[i] 的位置, ans[i] 为 -1 表示这样的位置不存在,比如前文提到的 2。那么此时的 ans 是 [-1,4,4,4,-1,-1,-1]。
第 8 步,我们又开始 pop 了。此时 pop 出来的是 9,因此 9 之后第一个小于 9 的索引便是 6。
这个算法的过程用一句话总结便是,如果压栈之后仍旧可以保持单调性,那么直接压。否则先弹出栈的元素,直到压入之后可以保持单调性。 这个算法的事理用一句话总结便是,被弹出的元素都是大于当前元素的,并且由于栈是单调减的,因此在其之后小于其本身的最近的便是当前元素了
下面给大家推举几道题,大家趁着知识还在脑筋来,赶紧去刷一下吧~
42. 接雨水(困难) 暴力解法、优化、双指针、单调栈
739. 逐日温度(中等) 暴力解法 + 单调栈
496. 下一个更大的元素 I(大略) 暴力解法、单调栈
316. 去除重复字母(困难) 栈 + 哨兵技巧(Java、C++、Python)
901. 股票价格跨度(中等) 「力扣」第 901 题:股票价格跨度(单调栈)
402. 移掉K位数字
581. 最短无序连续子数组
代码package 单调栈;import java.util.Arrays;import java.util.Stack;public class 第一个比自己大的元素 { public int[] findFirstLarger(int[] inputs) { int[] result = new int[inputs.length]; Stack<Integer> stack = new Stack<>(); Arrays.fill(result, -1); for (int i = 0; i < inputs.length; i++) { // 当第i个个位置的元素要比栈顶位置的元素大的时候,须要弹出栈顶的元素 while (!stack.empty() && inputs[i] > inputs[stack.peek()]) { Integer stackTopIndex = stack.pop(); result[stackTopIndex] = i - stackTopIndex; } stack.push(i); } return result; } public static void main(String[] args) { int[] input = {1, 3, 4, 5, 2, 9, 6}; int[] ints = new 第一个比自己大的元素().findFirstLarger(input); System.out.println(Arrays.toString(ints)); }}
繁芜度剖析
韶光繁芜度:由于 arr 的元素最多只会入栈,出栈一次,因此韶光繁芜度仍旧是 $O(N)$,个中 N 为数组长度。空间繁芜度:由于利用了栈, 并且栈的长度最大是和 arr 长度同等,因此空间繁芜度是 $O(N)$,个中 N 为数组长度。















