php输出等腰技巧_镶嵌画中的数学05三角形的密铺

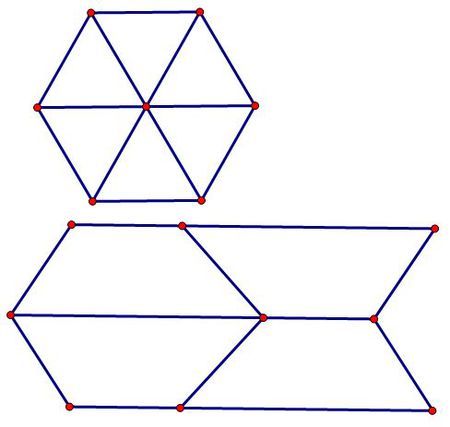
按理来说，三角形比四边形更加根本。
但之以是先讲完四边形，再讲三角形，是由于三角形密铺基本上都能由四边形密铺演化而来。
不相信？请听我逐步道来。

1. 任意三角形的密铺

我们在第二期讲过，平行四边形朝两个方向平移可以密铺平面。
将任意三角形旋转 180° 可以拼成一个平行四边形，因此任意三角形能密铺平面，如下图。

由于任意相邻两个三角形都是旋转 180° 的关系，因此根本三角形在变形时，需担保每条边都中央对称，这样其旋转 180° 之后才与自身重合。

密铺结果如下：

2. 等腰三角形

在任意三角形的密铺办法中，长边与长边重合，短边与短边重合，因此两个相邻三角形的公共边是同一条边。
而等腰三角形有两条边等长，因此一条公共边可以在这个三角形中是 AB，在另一个三角形中却是 AC。

照此思路，得到下图：

个中，每个三角形的两条边滑移反射，另一条边中央对称。

创造了吗，上图中两个等腰三角形组成的菱形，实际上是筝形密铺的变形特点——两组邻边滑移反射。

3. 等边三角形

连接正六边形的中央与 6 个顶点，可以将其分成 6 个等边三角形。
其余，如果结合上一期中的旋转密铺办法，我们自然想到：或容许以先将等边三角形其绕一个顶点旋转 5 次 60°，形成一个正六边形，然后再密铺平面。

照此思路，便能得到下图中的密铺办法：

个中，每个三角形的两条边旋转 60° 相同，第三条边中央对称。
你知道吗？埃舍尔的作品《对称水彩 94 条鱼》（1955）便是基于这种密铺办法的。

4. 等腰直角三角形

类似的，由于正方形可以由等腰直角三角形旋转拼成，因此存不才图的密铺办法：

个中，每个等腰直角三角形的两条边旋转 90° 相同，另一条边中央对称。

5. 120° 等腰三角形

同样地，等边三角形可以由含 120° 的等腰三角形旋转拼成，故存不才图的密铺办法：

个中，每个三角形的两条边旋转 120° 相同，另一条边中央对称。

在前几期文章中，我们先容了 5 种基于三角形的密铺和 12 种基于四边形的密铺。
在 Alain Nicolas 的 35 种密铺办法中，还有 5 种对称性很强的四边形密铺办法（即 1Sa、2Sa、2Sb、3Sa、4Sa），笔者认为其属于这 12 种密铺办法的分外情形，未将其单独列出。
是否妥当，还请读者评判。

接下来我们将先容基于六边形的密铺。
之以是先跳过五边形，一方面是由于某些五边形密铺以六边形密铺为根本，同时也由于五边形密铺问题比六边形密铺问题更加繁芜。

参考文献：

en.tessellations-nicolas.com/method.php