【欢迎关注、分享、点赞或评论,您的一个举手之劳,便是最大的鼓励!
】
欢迎关注【php在路上】每天进步一点。

码字不随意马虎,尊重版权,转载请注明出处:PHP在路上。
序言:提到算法,一定会谈论算法繁芜度。不少非打算机专业的程序员在参与算法谈论时,多少会有点尴尬(算法繁芜度到底是个什么东西)。
内容概要:1、算法繁芜度
2、韶光繁芜度
3、空间繁芜度
4、总结
一、算法繁芜度实在算法繁芜度是一个观点,一定程度上反响一个算法的好坏程度。算法繁芜度分为两个部分,韶光繁芜度和空间繁芜度。韶光繁芜度反应算法实行的韶光是非,空间繁芜度反应是算法占用内存(或叫存储空间)的大小。
必须说一下,所谓的繁芜度,不是一个详细的值,只是一个估值,在比较两种算法利害时利用。
二、韶光繁芜度
韶光繁芜度便是是一个函数,这个函数含有两个变量,一个算法的运行韶光,一个算法要处理数据的数量。
这里有一个关系:处理数据的数量越大,算法运行的次数和韶光越长。
假设处理数据的数量是n,算法运行的次数便是f(n)。这里的f()是一个函数,它的大小随着n增大而增大,数学上叫单调递增函数。
如果我们把算法的韶光繁芜度记为T(n);那他的值和算法运行的次数f(n)是有关的,随着n的增大,算法实行韶光的增长率和运行次数的增长率是正比例关系。以是f(n)越小,算法的质量越高,算法韶光繁芜度越低。
以是,在打算韶光繁芜度T(n)的时候,步骤如下:
1、先要拿出算法的基本单元。
2、根据相应的各语句确定它的实行次数f(n)。
3、找出T(n)的同数量级,将这个同数量等级赋值给f(n)。
4、由于T(n)/f(n)求极限可以得到一个常数C。(求极限值是高档数学内容,自行百度脑补一下),我们可以确定韶光的繁芜度T(n) = O(f(n));
个中,同数量等级有:1,Log2n ,n ,nLog2n ,n^2,n^3,2^n,n!,n^n。
总结:常用的韶光繁芜度所耗费的韶光从小到大依次是:O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)。随着问题规模n的不断增大,上述韶光繁芜度不断增大,算法的实行效率越低。
三、空间繁芜度
空间繁芜度是指算法在内存内所须要的存储空间的度量,一样平常是指除正常占用内存开销外的赞助存储单元规模。和韶光繁芜度类似,这样标记:S(n)=O(f(n))。
四、举例总结:
一样平常来说,韶光繁芜度和空间繁芜度还是比较难明得的。我们这里举例总结一下:
下面我们来举一个例子解释一下;看如下代码:
for(i=1;i<=n;++i{
for(j=1;j<=n;++j) {
c[ i ][ j ]=0; //基本单元 实行次数是n^2
for(k=1;k<=n;++k)
c[ i ][ j ]+=a[ i ][ k ]b[ k ][ j ]; //基本单元 实行次数是n^3(可以认为是三个for循环)
}
}
此时T(n)= n^2+n^3,我们这里取大的n^3(最大)作为T(n)的同数量级,则f(n)=n^3。由于T(n)/f(n)求极限可以得到常数C,则根据T(n)=O(f(n))=O(n^3);
一样平常情形下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
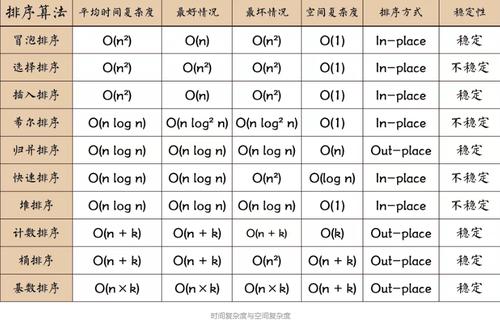
常见排序算法繁芜度
















