通过采取大学习率,我们可以在 70 个 epoch、不到 7000 次的迭代中,演习出准确率达到 93% 的模型(作为比拟,原论文的演习共有约为 360 个 epoch、64000 次迭代)。
下面供应的 Jupyter Notebook 中记录了所有的干系实验。实验中利用了和原论文相同的数据扩展:我们对图片进行了随机水平翻转;除此之外,我们在图片每边加入了 4 像素的添补,并进行随机裁剪。这里我们做出了一点小调度:我们没有利用玄色的添补像素,而是利用了反射添补(reflection padding),由于 fastai 库支持实现这种办法。这个调度大概能阐明为什么我们在利用和 Leslie 相同的超参数进行实验时,得到了比他稍好的结果。

Notebook 地址:https://github.com/sgugger/Deep-Learning/blob/master/Cyclical%20LR%20and%20momentums.ipynb
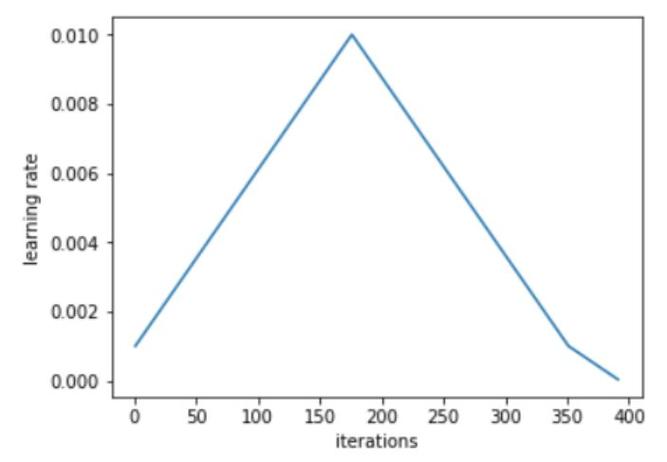
大学习率
可以通过这篇文章学习如何实现 Learning Rate Finder,这里简述如下:在开始演习模型的同时,从低到高地设置学习率,直到丢失(loss)变得失落控为止。然后将丢失和学习率画在一张图中,在丢失持续低落、即将达到最小值前的范围上取一个值作为学习率。下例中,可以在 10^-2 到 3×10^-2 之间任意取一个值。
这里的思想和 Leslie 是同等的,他在论文中提出了一个很好的演习方法。
Leslie 建议,用两个等长的步骤组成一个 cycle:从很小的学习率开始,逐步增大学习率,然后再逐步降落回最小值。最大学习率该当根据 Learning Rate Finder 来确定,最小值则可以取最大值的十分之一。这个 cycle 的长度该当比总的 epoch 次数略小,在演习的末了阶段,可以将学习率降落到最小值以下几个数量级。
从小学习率开始演习模型并不新颖:利用较小的学习率来预热演习是一种常用的方法,这也正是 Leslie 第一阶段的研究目标。Leslie 并不建议直接从大学习率开始,相反,他认为该当从低到高,缓慢地线性提升学习率,然后再用相同的韶光缓慢地降落回来。
Leslie 在实验中创造,在这个 cycle 的中间阶段,大学习率的效果类似于正则方法,可以抑制神经网络的过拟合。这是由于大学习率更偏好丢失函数上相对平缓的极小值,而防止模型收敛到一个陡峭区域上。在 Leslie 的另一篇论文中,他通过利用 1cycle,创造近似 Hessian 的方法会有更小的学习率,这意味着 SGD 搜索的是一个更平坦的区域。
在演习的末了阶段,通过降落学习率直到彻底消逝,可以得到丢失函数平滑区域中相对陡峭的局部极小值。
上图中,在 0 ~ 41 个 epoch 中,学习率从 0.08 提升到 0.8,在随后的 41 ~ 82 个 epoch 中,学习率降回 0.08,在末了的几次 epoch 中,学习率降落到 0.08 的百分之一。可以看到,在高学习率阶段(基本是 20 ~ 60 个 epoch),验证丢失表现得相对不稳定。但主要的是,均匀而言,演习偏差和验证偏差之间的间隔并没有增大。只有在 cycle 的末了阶段,学习率靠近为 0 时,才真正的涌现了过拟合。
令人惊异的是,通过 1cycle,我们乃至可以利用更高的最大学习率,即在根据 Learning Rate Finder 得到的图中,更靠近曲线最低点。这种演习会相对更加危险,由于丢失可能会骗你太远,以至于涌现严重的偏差;这时,在采取更低的学习率前,可以考试测验利用更长的 cycle:更长的预热过程该当会有所帮助。
上图中,在 0 ~ 22.5 个 epoch 中,学习率从 0.15 增加到 3;在 22.5~45 个 epoch 中降回到 0.15,在末了的几次 epoch 中,学习率降落到 0.15 的百分之一。通过利用这些非常高的学习率,学习完成得更快,同时也防止了过拟合。演习偏差和验证偏差之间的差距一贯保持在很低的水平,直到学习率靠近为 0。通过利用 1cycle 策略,可以仅仅经由 50 次 epoch,就在 cifar10 上演习出一个准确率 92.3% 的 resnet-56;我们可以利用包含 70 个 epoch 的 cycle 得到 93% 的准确率。
作为比拟,下图展示了利用更小的 cycle 以及更长收敛阶段的结果:
在这里,学习率变革的两个步骤在 42 个 epoch 中结束,剩下的演习过程中利用缓慢递减的学习率。这时验证偏差不再低落,进而涌现了越来越严重的过拟合征象,同时,准确率基本没有提升。
周期性动量
Leslie 在实验中还创造,在增大学习率的同时降落动量,可以得到更好的演习结果。这也印证了一个直觉:在演习中,我们希望 SGD 可以迅速调度到搜索平坦区域的方向上,因此就该当对新的梯度授予更大的权重。Leslie 建议,在真实场景中,可以选取如 0.85 和 0.95 的两个值,在增大学习率的时候,将动量从 0.95 降到 0.85,在降落学习率的时候,再将动量重新从 0.85 提升回 0.95。
据 Leslie 表示,利用根据完全演习选取的最优动量,也可以得到相同的终极结果;但利用周期性动量时,我们不须要摧残浪费蹂躏韶光去设立多个动量参数,然后进行多次完全演习来探求最优值。
虽然利用周期性动量确实能得到稍好的演习结果,但我并没有复现出 Leslie 论文中利用常动量值和利用周期性动量时的差异。
其他参数的影响
在演习中,调节模型其他超参数的办法也会影响最优学习率。因此在利用 Learning Rate Finder 时,一定要担保演习是在相同条件下完成的。例:不同的 batch 大小或权重衰减对结果的影响如下。
可以利用这个性子来设置一些超参数,如去做那种衰减率:Leslie 建议,可以在几组权重衰减率上运行 Learning Rate Finder,在能够接管利用高最大学习率进行演习的结果中,选择最大的一个。我们实验中选择的是 10^-4。
Leslie 认为,在内存可接管范围内,batch 越大越好。而其他可能包含的超参数(如 drop-out)则可以通过和权重衰减相同的方法来调节,或者直接根据一次 cycle 的结果来判断效果。但无论如何——尤其是当你决定采取一个靠近最大可能值的激进学习率时——一定要记住重跑 Learning Rate Finder。
高学习率的 1cycle 策略本身便是一种正则方法,以是在利用 1cycle 时,自然须要减少一些其他形式的常用正则项。但同它们比较,1cycle 的效率相对更高,由于在相称长的演习中,我们都利用了高学习率。
论文:A disciplined approach to neural network hyper-parameters: Part 1 -- learning rate, batch size, momentum, and weight decay
论文地址:https://arxiv.org/abs/1803.09820
择要:只管近年以来,深度学习已经在图像、语音、视频处理的运用处景中取得了令人瞩目的成功,但绝大部分演习所利用的超参数都是非最优的,因此不必要的延长了演习韶光。时至今日,超参数设置依然像一种邪术,须要依赖多年履历来完成。本文提出了一些设置超参数的高效方法,可以显著减少所需的演习韶光,并提升模型的表现效果。详细而言,本文展示了如何检测出演习在验证/测试丢失函数上轻微的欠拟合或过拟合,并给出了逼近最优平衡点的辅导建议。在接下来的部分,本文谈论了如何通过增加/减少学习率/动量来加速演习过程。试验结果表明,在每个数据集和架构上平衡正则的各个方面极其主要。我们以权重衰减作为正则项为例,展示了其最优值和学习率及动量间的紧密联系。
















