从旗子暗记的角度来看,这个天下是一个喧华的地方。为了弄清楚所有的事情,我们必须有选择地把把稳力集中到有用的信息上。
通过数百万年的自然选择过程,我们人类已经变得非常善于过滤背景旗子暗记。我们学会将特定的旗子暗记与特定的事宜联系起来。

例如,假设你正在繁忙的办公室中打乒乓球。为了还击对手的击球,你须要进行大量繁芜的打算和判断,将多个相互竞争的感官旗子暗记考虑进去。为了预测球的运动,你的大脑必须重复采样球的位置并估计它未来的轨迹。更厉害的球员还会将对手击球时施加的旋转考虑进去。末了,为了击球,你须要考虑对手的位置、自己的位置、球的速率,以及你打算施加的旋转。
所有这些都涉及到了大量的潜意识微分学。一样平常来说,我们天经地义的认为,我们的神经系统可以自动做到这些(至少经由一些练习之后)。
同样令人印象深刻的是,人类大脑是如何差异对待它所吸收到的无数竞争旗子暗记的主要性的。例如,球的位置被认为比你身后发生的对话或你面前打开的门更主要。
这听起来彷佛不值得一提,但实际上这证明了可以多大程度长进修从噪声数据中做出准确预测。
当然,一个被给予连续的视听数据流的空缺状态机将会面临一个困难的任务,即确定哪些旗子暗记能够最好地预测最佳行动方案。
幸运的是,有统计和打算方法可以用来识别带噪声和繁芜的数据中的模式。
干系性
一样平常来说,当我们谈到两个变量之间的「干系性(correlation)」时,在某种意义上,我们是指它们的「关系(relatedness)」。
干系变量是包含彼此信息的变量。两个变量的干系性越强,个中一个变量见告我们的关于另一个变量的信息就越多。
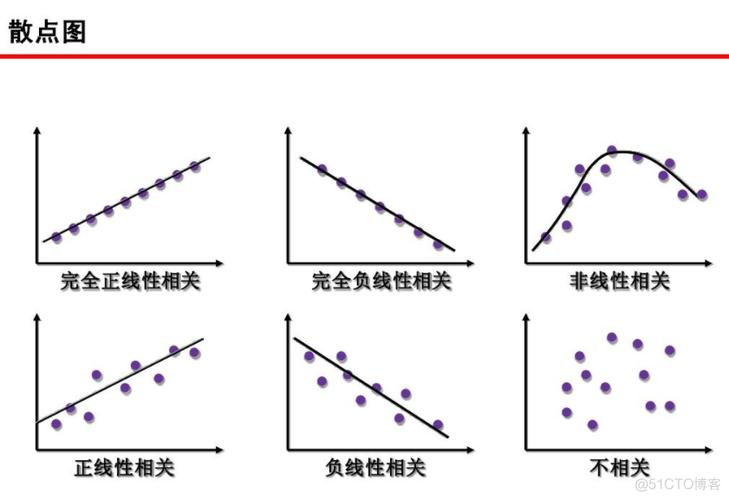
你可能之前就看过:正干系、零干系、负干系
你可能已经对干系性、它的浸染和它的局限性有了一定理解。事实上,这是一个数据科学的旧调重弹:
「干系性不虞味着因果关系」
这当然是精确的——有充分的情由解释,纵然是两个变量之间有强干系性也不担保存在因果关系。不雅观察到的干系性可能是由于隐蔽的第三个变量的影响,或者完备是有时的。
也便是说,干系性确实许可基于另一个变量来预测一个变量。有几种方法可以用来估计线性和非线性数据的干系性。我们来看看它们是如何事情的。
我们将用 Python 和 R 来进行数学和代码实现。本文示例的代码可以在这里找到:
GitHub https://gist.github.com/anonymous/fabecccf33f9c3feb568384f626a2c07
皮尔逊干系系数
皮尔逊干系系数(PCC, 或者 Pearson's r)是一种广泛利用的线性干系性的度量,它常日是很多低级统计课程的第一课。从数学角度讲,它被定义为「两个向量之间的协方差,通过它们标准差的乘积来归一化」。
两个成对的向量之间的协方差是它们在均值高下颠簸趋势的一种度量。也便是说,衡量一对向量是否方向于在各自均匀值的同侧或相反。
让我们看看在 Python 中的实现:
def mean(x):
return sum(x)/len(x)
def covariance(x,y):
calc = []
for i in range(len(x)):
xi = x[i] - mean(x)
yi = y[i] - mean(y)
calc.append(xi yi)
return sum(calc)/(len(x) - 1)
a = [1,2,3,4,5] ; b = [5,4,3,2,1]
print(covariance(a,b))
协方差的打算方法是从每一对变量中减去各自的均值。然后,将这两个值相乘。
如果都高于(或都低于)均值,那么结果将是一个正数,由于正数 × 正数 = 正数;同样的,负数 × 负数 = 负数。
如果在均值的不同侧,那么结果将是一个负数(由于正数 × 负数 = 负数)。
一旦我们为每一对变量都打算出这些值,将它们加在一起,并除以 n-1,个中 n 是样今年夜小。这便是样本协方差。
如果这些变量都方向于分布在各自均值的同一侧,协方差将是一个正数;反之,协方差将是一个负数。这种方向越强,协方差的绝对值就越大。
如果不存在整体模式,那么协方差将会靠近于零。这是由于正值和负值会相互抵消。
最初,协方差彷佛是两个变量之间「关系」的充分度量。但是,请看下面的图:
协方差 = 0.00003
看起来变量之间有很强的关系,对吧?那为什么协方差这么小呢(大约是 0.00003)?
这里的关键是要认识到协方差是依赖于比例的。看一下 x 和 y 坐标轴——险些所有的数据点都落在了 0.015 和 0.04 之间。协方差也将靠近于零,由于它是通过从每个个体不雅观察值中减去均匀值来打算的。
为了得到更故意义的数字,归一化协方差是非常主要的。方法是将其除以两个向量标准差的乘积。
在希腊字母中 ρ 常用来表示皮尔逊干系系数
在 Python 中:
import math
def stDev(x):
variance = 0
for i in x:
variance += (i - mean(x) 2) / len(x)
return math.sqrt(variance)
def Pearsons(x,y):
cov = covariance(x,y)
return cov / (stDev(x) stDev(y))
这样做的缘故原由是由于向量的标准差是是其方差的平方根。这意味着如果两个向量是相同的,那么将它们的标准差相乘就即是它们的方差。
有趣的是,两个相同向量的协方差也即是它们的方差。
因此,两个向量之间协方差的最大值即是它们标准差的乘积(当向量完备干系时会涌现这种情形)。这将干系系数限定在 -1 到 +1 之间。
箭头指向哪个方向?
顺便说一下,一个定义两个向量的 PCC 的更酷的方法来自线性代数。
首先,我们通过从向量各自的值中减去其均值的方法来「集中」向量。
a_centered = [i - mean(a) for i in a]
b_centered = [j - mean(b) for j in b]
现在,我们可以利用向量可以看做指向特定方向的「箭头」的事实。
例如,在 2-D 空间中,向量 [1,3] 可以代表一个沿 x 轴 1 个单位,沿 y 轴 3 个单位的箭头。同样,向量 [2,1] 可以代表一个沿 x 轴 2 个单位,沿 y 轴 1 个单位的箭头。
两个向量 (1,3) 和 (2,1) 如箭头所示。
类似地,我们可以将数据向量表示为 n 维空间中的箭头(只管当 n > 3 时不能考试测验可视化)。
这些箭头之间的角度 可以利用两个向量的点积来打算。定义为:
或者,在 Python 中:
def dotProduct(x,y):
calc = 0
calc += x[i] y[i]
return calc
点积也可以被定义为:
个中 || x || 是向量 x 的大小(或「长度」)(参考勾股定理), 是箭头向量之间的角度。
正如一个 Python 函数:
def magnitude(x):
x_sq = [i 2 for i in x]
return math.sqrt(sum(x_sq))
我们通过将点积除以两个向量大小的乘积的方法得到 cos()。
def cosTheta(x,y):
mag_x = magnitude(x)
mag_y = magnitude(y)
return dotProduct(x,y) / (mag_x mag_y)
现在,如果你对三角学有一定理解,你可能会记得,余弦函数产生一个在 +1 和 -1 之间震荡的图形。
cos() 的值将根据两个箭头向量之间的角度而发生变革。
当角度为零时(即两个向量指向完备相同的方向),cos() 即是 1。
当角度为 -180°时(两个向量指向完备相反的方向),cos() 即是 -1。
当角度为 90°时(两个向量指向完备不干系的方向),cos() 即是 0。
这可能看起来很熟习——一个介于 +1 和 -1 之间的衡量标准彷佛描述了两个向量之间的关系?那不是 Pearson’s r 吗?
那么——这正是它的阐明!
通过将数据视为高维空间中的箭头向量,我们可以用它们之间的角度 作为相似度的衡量。
A) 正干系向量; B) 负干系向量; C) 不干系向量
该角度 的余弦在数学上与皮尔逊干系系数相等。当被视为高维箭头时,正干系向量将指向一个相似的方向。负干系向量将指向相反的方向。而不干系向量将指向直角。
就我个人而言,我认为这是一个理解干系性的非常直不雅观的方法。
统计显著性?
正如频率统计一样,主要的是讯问从给定样本打算的考验统计量实际上有多主要。Pearson's r 也不例外。
不幸的是,PCC 估计的置信区间不是完备直接的。
这是由于 Pearson's r 被限定在 -1 和 +1 之间,因此不是正态分布的。而估计 PCC,例如 +0.95 之上只有很少的容错空间,但在其之下有大量的容错空间。
幸运的是,有一个办理方案——用一个被称为 Fisher 的 Z 变换的技巧:
像平常一样打算 Pearson's r 的估计值。
用 Fisher 的 Z 变换将 r→z,用公式 z = arctanh(r) 完成。
现在打算 z 的标准差。幸运的是,这很随意马虎打算,由 SDz = 1/sqrt(n-3) 给出,个中 n 是样今年夜小。
选择显著性阈值,alpha,并检讨与此对应的均匀值有多少标准差。如果取 alpha = 0.95,用 1.96。
通过打算 z +(1.96 × SDz) 找到上限,通过打算 z - (1.96 × SDz) 找到下限。
用 r = tanh(z) 将这些转换回 r。
如果上限和下限都在零的同一侧,则有统计显著性!
这里是在 Python 中的实现:
r = Pearsons(x,y)
z = math.atanh(r)
SD_z = 1 / math.sqrt(len(x) - 3)
z_upper = z + 1.96 SD_z
z_lower = z - 1.96 SD_z
r_upper = math.tanh(z_upper)
r_lower = math.tanh(z_lower)
当然,当给定一个包含许多潜在干系变量的大数据集时,检讨每对的干系性可能很吸引人。这常日被称为「数据疏通」——在数据集中查找变量之间的任何明显关系。
如果确实采取这种多重比较方法,则该当用适当的更严格的显著性阈值来降落创造缺点干系性的风险(即找到纯粹有时干系的无关变量)。
一种方法是利用 Bonferroni correction。
小结
到现在为止还好。我们已经看到 Pearson's r 如何用来打算两个变量之间的干系系数,以及如何评估结果的统计显著性。给定一组未知的数据,用于开始挖掘变量之间的主要关系是很有可能的。
但是,有一个主要的陷阱——Pearson's r 只适用于线性数据。
看下面的图。它们清楚地展示了一种看似非随机的关系,但是 Pearson's r 非常靠近于零。
缘故原由是由于这些图中的变量具有非线性关系。
我们常日可以将两个变量之间的关系描述成一个点云,分散在一条线的两侧。点云的分散度越大,数据越「喧华」,关系越弱。
然而,由于它将每个单独的数据点与整体均匀值进行比较,以是 Pearson's r 只考虑直线。这意味着检测非线性关系并不是很好。
在上面的图中,Pearson's r 并没有显示研究工具的干系性。
然而,这些变量之间的关系很显然是非随机的。幸运的是,我们有不同的干系性方法。
让我们来看看个中几个。
间隔干系性
间隔干系性与 Pearson's r 有一些相似之处,但是实际上是用一个相称不同的协方差观点来打算的。该方法通过用「间隔」类似物替代常用的协方差和标准差(如上所定义)的观点。
类似 Pearson's r,「间隔干系性」被定义为「间隔协方差」,由「间隔标准差」来归一化。
间隔干系性不是根据它们与各自均匀值的间隔来估计两个变量如何共同变革,而是根据与其他点的间隔来估计它们是如何共同变革的,从而能更好捕捉变量之间非线性依赖关系。
深入细节
出生于 1773 年的 Robert Brown 是一名苏格兰植物学家。当布朗在显微镜下研究植物花粉时,把稳到液面上有随机运动的有机颗粒。
他没有想到,这一不雅观察竟使他名垂千古——他成为了布朗运动的(重新)创造者。
他更不会知道,近一个世纪的韶光后爱因斯坦才对这种征象做出理解释,从而证明了原子的存在。同年,爱因斯坦揭橥了关于狭义相对论的论文(E=MC),并打开了量子理论的大门。
布朗运动是这样一个物理过程:由于与周围粒子的碰撞,眇小粒子随机运动。
布朗运动背后的数学事理可以被推广为维纳过程(Weiner process),维纳过程在数学金融中最著名的模型 Black-Scholes 中也扮演着重要的角色。
有趣的是,Gabor Szekely 在 20 世纪中期的研究表明,布朗运动和维纳过程和一个非线性关联度量干系。
让我们来看看如何由长度为 N 的向量 x 和 y 打算这个量。
1. 首先,我们对每个向量构建 N×N 的间隔矩阵。间隔矩阵和舆图中的道路间隔表非常类似——每行、每列的交点显示了相应城市间的间隔。在间隔矩阵中,行 i 和列 j 的交点给出了向量的第 i 个元素和第 j 个元素之间的间隔。
2. 第二,矩阵是「双中央」的。也便是说,对付每个元素,我们减去了它的行均匀值和列均匀值。然后,我们再加上全体矩阵的总均匀值。
上述公式中,加「^」表示「双中央」,加「-」表示「均匀值」。
3. 在两个双中央矩阵的根本上,将 X 中每个元素的均值乘以 Y 中相应元素的均值,则可打算出间隔协方差的平方。
4. 现在,我们可以用类似的办法找到「间隔方差」。请记住,若两个向量相同,其协方差与其方差相等。因此,间隔方差可表示如下:
5. 末了,我们利用上述公式打算间隔干系性。请记住,(间隔)标准差与(间隔)方差的平方根相等。
如果你更喜好代码实现而非数学符号,那么请看下面的 R 措辞实现:
set.seed(1234)
doubleCenter <- function(x){
centered <- x
for(i in 1:dim(x)[1]){
for(j in 1:dim(x)[2]){
centered[i,j] <- x[i,j] - mean(x[i,]) - mean(x[,j]) + mean(x)
}
}
return(centered)
}
distanceCovariance <- function(x,y){
N <- length(x)
distX <- as.matrix(dist(x))
distY <- as.matrix(dist(y))
centeredX <- doubleCenter(distX)
centeredY <- doubleCenter(distY)
calc <- sum(centeredX centeredY)
return(sqrt(calc/(N^2)))
}
distanceVariance <- function(x){
return(distanceCovariance(x,x))
}
distanceCorrelation <- function(x,y){
cov <- distanceCovariance(x,y)
sd <- sqrt(distanceVariance(x)distanceVariance(y))
return(cov/sd)
}
# Compare with Pearson's r
x <- -10:10
y <- x^2 + rnorm(21,0,10)
cor(x,y) # --> 0.057
distanceCorrelation(x,y) # --> 0.509
任意两变量的间隔干系性都在 0 和 1 之间。个中,0 代表两变量相互独立,而靠近于 1 则表明变量间存在依赖关系。
如果你不想从头开始编写间隔干系方法,你可以安装 R 措辞的 energy 包(https://cran.r-project.org/web/packages/energy/index.html),设计此方案的研究者供应了本代码。在该程序包中,各种可用方案调用的是 C 措辞编写的函数,因此有着很大的速率上风。
物理解释
关于间隔干系性的表述,有着一个更令人惊异的结果——它与布朗关联(Brownian correlation)有着确切的等价关系。
布朗关联指的是两个布朗过程之间的独立性(或依赖性)。相互依赖的布朗过程将会表现出彼此「跟随」的趋势。
让我们用一个大略的比喻来把握间隔干系性的观点——请看下图中漂浮在湖面上的小纸船。
如果没有盛行风向,那么每艘船都将进行随机漂流——这与布朗运动类似。
无盛行风向时,小船随机漂流
如果存在盛行风向,那么小船漂流的方向将依赖于风的强度。风力越强,依赖性越显著。
有盛行风向时,小船方向于同向漂流
与之类似,无关变量可以被看作无盛行风向时随机漂流的小船;干系变量可以被看作在盛行风向影响下漂流的小船。在这个比喻中,风的强弱就代表着两个变量之间干系性的强弱。
如果我们许可盛行风向在湖面的不同位置有所不同,那么我们就可以引入非线性的观点。间隔干系性利用「小船」之间的间隔推断盛行风的强度。
置信区间?
我们可以采纳「重采样(resampling)」方法为间隔干系性估计建立置信区间。一个大略的例子是 bootstrap 重采样。
这是一个奥妙的统计技巧,须要我们从原始数据集中随机抽样(更换)以「重修」数据。这个过程将重复多次(例如 1000 次),每次都打算感兴趣的统计量。
这将为我们感兴趣的统计量产生一系列不同的估计值。我们可以通过它们估计在给定置信水平下的上限和下限。
请看下面的 R 措辞代码,它实现了大略的 bootstrap 函数:
bootstrap <- function(x,y,reps,alpha){
estimates <- c()
original <- data.frame(x,y)
N <- dim(original)[1]
for(i in 1:reps){
S <- original[sample(1:N, N, replace = TRUE),]
estimates <- append(estimates, distanceCorrelation(S$x, S$y))
}
u <- alpha/2 ; l <- 1-u
interval <- quantile(estimates, c(l, u))
return(2(dcor(x,y)) - as.numeric(interval[1:2]))
}
# Use with 1000 reps and threshold alpha = 0.05
bootstrap(x,y,1000,0.05) # --> 0.237 to 0.546
如果你想建立统计显著性,还有另一个重采样技巧,名为「排列考验(permutation test)」。
排列考验与上述 bootstrap 方法略有不同。在排列考验中,我们保持一个向量不变,并通过重采样对另一个变量进行「洗牌」。这靠近于零假设(null hypothesis)——即,在变量之间不存在依赖关系。
这个经「洗牌」打乱的变量将被用于打算它和常变量间的间隔干系性。这个过程将被实行多次,然后,结果的分布将与实际间隔干系性(从未被「洗牌」的数据中得到)比较较。
然后,大于或即是「实际」结果的经「洗牌」的结果的比例将被定为 P 值,并与给定的显著性阈值(如 0.05)进行比较。
以下是上述过程的代码实现:
permutationTest <- function(x,y,reps){
observed <- distanceCorrelation(x,y)
y_i <- sample(y, length(y), replace = T)
estimates <- append(estimates, distanceCorrelation(x, y_i))
}
p_value <- mean(estimates >= observed)
return(p_value)
}
# Use with 1000 reps
permutationTest(x,y,1000) # --> 0.036
最大信息系数
最大信息系数(MIC)于 2011 年提出,它是用于检测变量之间非线性干系性的最新方法。用于进行 MIC 打算的算法将信息论和概率的观点运用于连续型数据。
深入细节
由克劳德·喷鼻香农于 20 世纪中叶首创的信息论是数学中一个引人瞩目的领域。
信息论中的一个关键观点是熵——这是一个衡量给定概率分布的不愿定性的度量。概率分布描述了与特定事宜干系的一系列给定结果的概率。
概率分布的熵是「每个可能结果的概率乘以其对数后的和」的负值
为了理解其事情事理,让我们比较下面两个概率分布:
X 轴标明了可能的结果;Y 轴标明了它们各自的概率
左侧是一个常规六面骰子结果的概率分布;而右边的六面骰子不那么均匀。
从直觉上来说,你认为哪个的熵更高呢?哪个骰子结果的不愿定性更大?让我们来打算它们的熵,看看答案是什么。
entropy <- function(x){
pr <- prop.table(table(x))
H <- sum(pr log(pr,2))
return(-H)
}
dice1 <- 1:6
dice2 <- c(1,1,1,1,2:6)
entropy(dice1) # --> 2.585
entropy(dice2) # --> 2.281
不出所料,常规骰子的熵更高。这是由于每种结果的可能性都一样,以是我们不会提前知道结果倾向哪个。但是,非常规的骰子有所不同——某些结果的发生概率远大于其它结果——以是它的结果的不愿定性也低一些。
这么一来,我们就能明白,当每种结果的发生概率相同时,它的熵最高。而这种概率分布也便是传说中的「均匀」分布。
交叉熵是熵的一个拓展观点,它引入了第二个变量的概率分布。
crossEntropy <- function(x,y){
prX <- prop.table(table(x))
prY <- prop.table(table(y))
H <- sum(prX log(prY,2))
}
两个相同概率分布之间的交叉熵即是其各自单独的熵。但是对付两个不同的概率分布,它们的交叉熵可能跟各自单独的熵有所不同。
这种差异,或者叫「散度」可以通过 KL 散度(Kullback-Leibler divergence)量化得出。
两概率分布 X 与 Y 的 KL 散度如下:
概率分布 X 与 Y 的 KL 散度即是它们的交叉熵减去 X 的熵
KL 散度的最小值为 0,仅当两个分布相同。
KL_divergence <- function(x,y){
kl <- crossEntropy(x,y) - entropy(x)
return(kl)
}
为了创造变量具有干系性,KL 散度的用场之一是打算两个变量的互信息(MI)。
互信息可以定义为「两个随机变量的联合分布和边缘分布之间的 KL 散度」。如果二者相同,MI 值取 0。如若不同,MI 值就为一个正数。二者之间的差异越大,MI 值就越大。
为了加深理解,我们首先大略回顾一些概率论的知识。
变量 X 和 Y 的联合概率便是二者同时发生的概率。例如,如果你抛掷两枚硬币 X 和 Y,它们的联合分布将反响抛掷结果的概率。假设你抛掷硬币 100 次,得到「正面、正面」的结果 40 次。联合分布将反响如下:
P(X=H, Y=H) = 40/100 = 0.4
jointDist <- function(x,y){
u <- unique(append(x,y))
joint <- c()
for(i in u){
for(j in u){
f <- x[paste0(x,y) == paste0(i,j)]
joint <- append(joint, length(f)/N)
}
}
return(joint)
}
边缘分布是指不考虑其它变量而只关注某一特定变量的概率分布。假设两变量独立,二者边缘概率的乘积即为二者同时发生的概率。仍以抛硬币为例,如果抛掷结果是 50 次正面和 50 次反面,它们的边缘分布如下:
P(X=H) = 50/100 = 0.5 ; P(Y=H) = 50/100 = 0.5
P(X=H) × P(Y=H) = 0.5 × 0.5 = 0.25
marginalProduct <- function(x,y){
marginal <- c()
fX <- length(x[x == i]) / N
fY <- length(y[y == j]) / N
marginal <- append(marginal, fX fY)
}
return(marginal)
}
现在让我们回到抛硬币的例子。如果两枚硬币相互独立,边缘分布的乘积表示每个结果可能发生的概率,而联合分布则为实际得到的结果的概率。
如果两硬币完备独立,它们的联合概率在数值上(约)即是边缘分布的乘积。若只是部分独立,此处就存在散度。
这个例子中,P(X=H,Y=H) > P(X=H) × P(Y=H)。这表明两硬币全为正面的概率要大于它们的边缘分布之积。
联合分布和边缘分布乘积之间的散度越大,两个变量之间干系的可能性就越大。两个变量的互信息定义了散度的度量办法。
X 和 Y 的互信息即是「二者边缘分布积和的联合分布的 KL 散度」
mutualInfo <- function(x,y){
joint <- jointDist(x,y)
marginal <- marginalProduct(x,y)
Hjm <- - sum(joint[marginal > 0] log(marginal[marginal > 0],2))
Hj <- - sum(joint[joint > 0] log(joint[joint > 0],2))
return(Hjm - Hj)
}
此处的一个主要假设便是概率分布是离散的。那么我们如何把这些观点运用到连续的概率分布呢?
分箱算法
个中一种方法是量化数据(使变量离散化)。这是通过分箱算法(bining)实现的,它能将连续的数据点分配对应的离散种别。
此方法的关键问题是到底要利用多少「箱子(bin)」。幸运的是,首次提出 MIC 的论文给出了建议:穷举!
也便是说,去考试测验不同的「箱子」个数并不雅观测哪个会在变量间取到最大的互信息值。不过,这提出了两个寻衅:
要试多少个箱子呢?理论上你可以将变量量化到任意间距值,可以使箱子尺寸越来越小。
互信息对所用的箱子数很敏感。你如何公正比较不同箱子数目之间的 MI 值?
第一个寻衅从理论上讲是不能做到的。但是,论文作者供应了一个启示式解法(也便是说,解法不完美,但是十分靠近完美解法)。他们也给出了可试箱子个数的上限。
最大可用箱子个数由样本数 N 决定
至于如何公正比较取不同箱子数对 MI 值的影响,有一个大略的做法……便是归一化!
这可以通过将每个 MI 值除以在特定箱子数组合上取得的理论最大值来完成。我们要采取的是产生最大归一化 MI 总值的箱子数组合。
互信息可以通过除以最小的箱子数的对数来归一化
最大的归一化互信息便是 X 和 Y 的最大信息系数(MIC)。我们来看看一些估算两个连续变量的 MIC 的代码。
MIC <- function(x,y){
maxBins <- ceiling(N 0.6)
MI <- c()
for(i in 2:maxBins) {
for (j in 2:maxBins){
if(i j > maxBins){
next
Xbins <- i; Ybins <- j
binnedX <-cut(x, breaks=Xbins, labels = 1:Xbins)
binnedY <-cut(y, breaks=Ybins, labels = 1:Ybins)
MI_estimate <- mutualInfo(binnedX,binnedY)
MI_normalized <- MI_estimate / log(min(Xbins,Ybins),2)
MI <- append(MI, MI_normalized)
}
}
return(max(MI))
}
x <- runif(100,-10,10)
y <- x2 + rnorm(100,0,10)
MIC(x,y) # --> 0.751
以上代码是对原论文中方法的简化。更靠近原作的算法实现可以参考 R package minerva(https://cran.r-project.org/web/packages/minerva/index.html)。
在 Python 中的实现请参考 minepy module(https://minepy.readthedocs.io/en/latest/)。
MIC 能够表示各种线性和非线性的关系,并已得到广泛运用。它的值域在 0 和 1 之间,值越高表示干系性越强。
置信区间?
为了建立 MIC 估计值的置信区间,你可以大略地利用一个像我们之前先容过的 bootstrap 函数。我们可以利用 R 措辞的函数式编程,通过通报我们想要用作参数的函数来泛化 bootstrap 函数。
bootstrap <- function(x,y,func,reps,alpha){
estimates <- append(estimates, func(S$x, S$y))
}
l <- alpha/2 ; u <- 1 - l
interval <- quantile(estimates, c(u, l))
return(2(func(x,y)) - as.numeric(interval[1:2]))
}
bootstrap(x,y,MIC,100,0.05) # --> 0.594 to 0.88
总结
为了总结干系性这一主题,我们来测试下各算法在人工天生数据上的处理能力。
完全代码:https://gist.github.com/anonymous/fabecccf33f9c3feb568384f626a2c07
噪声函数
set.seed(123)
# Noise
x0 <- rnorm(100,0,1)
y0 <- rnorm(100,0,1)
plot(y0~x0, pch = 18)
cor(x0,y0)
distanceCorrelation(x0,y0)
MIC(x0,y0)
Pearson'sr = - 0.05
间隔干系性 = 0.157
MIC = 0.097
大略线性函数
# Simple linear relationship
x1 <- -20:20
y1 <- x1 + rnorm(41,0,4)
plot(y1~x1, pch =18)
cor(x1,y1)
distanceCorrelation(x1,y1)
MIC(x1,y1)
Pearson's r=+0.95
间隔干系性 = 0.95
MIC = 0.89
大略二次函数
# y ~ x2
x2 <- -20:20
y2 <- x22 + rnorm(41,0,40)
plot(y2~x2, pch = 18)
cor(x2,y2)
distanceCorrelation(x2,y2)
MIC(x2,y2)
Pearson's r =+0.003
间隔干系性 = 0.474
MIC = 0.594
三次函数
# Cosine
x3 <- -20:20
y3 <- cos(x3/4) + rnorm(41,0,0.2)
plot(y3~x3, type='p', pch=18)
cor(x3,y3)
distanceCorrelation(x3,y3)
MIC(x3,y3)
Pearson's r=- 0.035
间隔干系性 = 0.382
MIC = 0.484
圆函数
# Circle
n <- 50
theta <- runif (n, 0, 2pi)
x4 <- append(cos(theta), cos(theta))
y4 <- append(sin(theta), -sin(theta))
plot(x4,y4, pch=18)
cor(x4,y4)
distanceCorrelation(x4,y4)
MIC(x4,y4)
Pearson's r< 0.001
间隔干系性 = 0.234
MIC = 0.218
原文链接:https://medium.freecodecamp.org/how-machines-make-predictions-finding-correlations-in-complex-data-dfd9f0d87889
本文为机器之心编译,转载请联系本"大众年夜众号得到授权。
















